1.1. Система отсчёта. Язык кинематики. Динамика. Общие замечания

1. ВВЕДЕНИЕ

Физика представляет собой науку о простейших и вместе с тем наиболее общих формах движения материи и законах природы. В современном естествознании физика — одна из ведущих наук о природе, поскольку с помощью физики можно объяснить основные химические процессы, понять многие биологические закономерности и даже описать элементы самоорганизации в природе.

Слово “физика” происходит от греческого понятия “physis”, то есть природа. Во времена Аристотеля (384-322 гг. до нашей эры), патриарха физики, предметом исследования была совокупность всех природных явлений.

Развитие физики в современном понимании началось в XVII веке и, в первую очередь, связано с именами Г. Галилея (1564-1642 гг.) и И. Ньютона (1643-1727 гг.). Именно эти великие учёные заложили начала классической физики — механики (классическая механика), которая часто называется механикой Галилея-Ньютона. Её основополагающим отличием от учения Аристотеля является наличие математического описания движения и представление о том, что воздействие на исследуемое тело других объектов определяет не скорость (как считалось в учении Аристотеля), а ускорение тела.

Дальнейшее развитие физики показало, что классическая механика, описывающая движение только макроскопических тел со скоростями значительно меньшими, чем скорость света в вакууме (с=3×108 м/с), является частным случаем релятивистской механики, когда скорости тела сравнимы со скоростью света. Эта новая механика основана на специальной теории относительности А. Эйнштейна.

Для рассмотрения движения микрочастиц необходимо введение квантовой механики, где используются совсем иные законы и понятия.

2. СИСТЕМА ОТСЧЁТА. ЯЗЫК КИНЕМАТИКИ

Классическая механика — раздел физики, в котором изучаются закономерности механического движения тел и причины, влияющие на это движение. При этом под механическим движением обычно понимается изменение взаимного расположения тел или их частей относительно друг друга с течением времени.

Физика, как и любая другая наука, использует при рассмотрении конкретных ситуаций довольно много весьма полезных приближений — абстракций. Например, при решении целого ряда задач, связанных с движением тела пренебрегают его деформацией, вводя понятие абсолютно твёрдого тела, у которого взаимное расположение его частиц не меняется при движении, или используют понятие материальная точка, под которой имеют в виду тело, размерами которого в данной задаче можно пренебречь, а внутреннюю структуру не учитывать.

Механика обычно делится на три больших раздела: кинематику, динамику и статику.

Кинематика изучает движение тел без учёта причин, вызывающих и изменяющих движение. Динамика эти причины исследует, формируя законы движения. Статика рассматривает условия равновесия тел и, по сути, законы статики являются частным случаем законов динамики.

Наша первая лекция посвящена кинематике. Остановимся на основных понятиях этого раздела.

Механическое движение относительно. Говоря о движении какого-либо тела, необходимо указать относительно каких других тел перемещается рассматриваемый объект. Тело (или совокупность тел), которое условно считается неподвижным и по отношению к которому рассматривается движение других тел называется телом отсчёта. Движение тел рассматривают в системе отсчёта, представляющей собой тело отсчёта, жестко связанную с ним систему координат и выбранный способ измерения времени.

Пример. Пусть материальная точка переместилась за время Dt из позиции N в позицию M, которые мы фиксируем в прямоугольной (декартовой) системе координат, рис. 1.1.

В заданный момент времени положение точки по отношению к этой системе характеризуется тремя координатами x, y, z или радиусом-вектором r(t), проведённым из начала координат в данную точку.

Совокупность последовательных положений, которые занимает материальная точка при своём движении, называется траекторией (годограф вектора r(t)).

Путь — это неотрицательная скалярная величина, равная расстоянию, пройденному материальной точкой вдоль её траектории (s или в обозначении на рис. 1.1 — Ds).

Вектор Dr, проведённый из начального положения движущейся точки (в момент времени t, см. рис. 1.1) в положение, занимаемое ей в данный момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени Dt), называется перемещением (при этом r(t+Dt)=r(t)+Dr).

При прямолинейном движении модуль перемещения |Dr| равен пройденному телом пути Ds, если движение происходило в неизменном направлении.

Векторную величину, характеризующую направление и быстроту перемещения материальной точки относительно тела отсчёта, называют скоростью. В нашем случае

Таким образом, мгновенная скорость v есть векторная величина, равная первой производной радиуса-вектора движущейся материальной точки по времени. В пределе (см. рис. 1.1) вектор v будет совпадать с касательной к траектории в направлении движения, путь

которую на транспорте называют маршрутной скоростью (маршрутная скорость московского метро составляет около 40 км/ч).

Пример. Катер двигался по течению реки из пункта А в пункт Б со скоростью u1, а обратно со скоростью u2. Найти маршрутную скорость катера при движении.

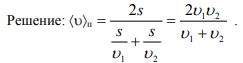
Скорость тел при движении может изменяться. Физическую величину, характеризующую быстроту изменения скорости по модулю и направлению, назвали ускорением.

Средним ускорением является отношение

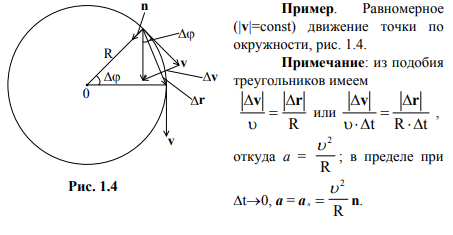
Как показывает эксперимент, вектор ускорения при криволинейном движении направлен под произвольным углом к направлению вектора скорости (рис. 1.2, подробнее в динамике). Его можно разложить на две составляющих: at — касательное или тангенциальное ускорение и an — нормальное или центростремительное ускорение, то есть

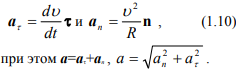
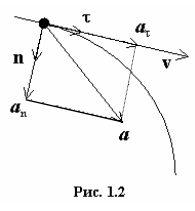
В данном случае t и n — единичные векторы в направлении соответственно вдоль и перпендикулярно вектору скорости, R — радиус кривизны траектории. Дело в том, что любой небольшой участок произвольно искривленной линии можно приближённо рассматривать как дугу окружности, которая будет сливаться с линией на бесконечно малом её участке. Радиус этой окружности и получил название радиуса кривизны траектории.

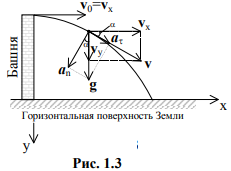
Нормальное ускорение an характеризует быстроту изменения скорости по направлению, касательное at – по модулю. Пример. Баллистическое движение, рис. 1.3.

Примечание: для случая свободного падения (в вакууме) Галилей постулировал, что все тела будут падать с одинаковым постоянным ускорением g, его значение равно g»9,8 м/c2.

3. ВИДЫ ДВИЖЕНИЯ

Общие замечания

Реальное движение тел обычно носит сложный характер. Для упрощения задачи пользуются законом независимости движений, согласно которому любое сложное движение можно представить как результат наложения независимых простейших движений. Например, простейшими движениями являются поступательное и вращательное.

В первом, поступательном движении все точки тела движутся по траекториям одинаковой формы и при этом имеют одинаковые скорости и ускорения. В этом плане рассмотрение поступательного движения тела удобно свести к изучению движения материальной точки. По виду траектории поступательное движение можно разделить на два типа движений: прямолинейное движение (траектория — прямая линия) и криволинейное, где траектория представляет собой произвольную кривую.

Во втором, вращательном движении все точки абсолютно твёрдого тела движутся по окружностям, центры которых находятся на одной прямой, называемой осью вращения, при этом окружности лежат в плоскостях, перпендикулярных этой оси.

Примером сложного движения, которое можно разбить на поступательную и вращательную составляющие является движение колеса по дороге.

Если материальная точка участвует одновременно в нескольких движениях, то результирующее перемещение и результирующая скорость находятся по правилу сложения векторов.

Равномерное движение

Если материальная точка за равные, сколь угодно малые промежутки времени, проходит одинаковые пути, то такое её движение называется равномерным (u=const).

В случае равномерного прямолинейного движения сохраняется и направление вектора скорости, то есть

v=const

Согласно (1.5) модуль вектора скорости можно представить как первую производную от пути по времени, откуда

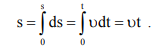
Пример. Материальная точка равномерно движется вдоль прямой. Если ось координат x взять вдоль направления движения, то проекция скорости точки ux ,будет равна величине вектора скорости ux=u, поэтому, опуская индекс x, запишем

где под u уже однозначно понимают модуль вектора скорости, или же в выражении (1.15) сохраняют знак плюс, в таком случае считая u величиной вектора скорости.

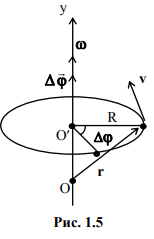
Рассмотрим равномерное движение при вращении какого-либо тела, выделяя в нём конкретную точку, поворачивающуюся относительно, например, оси y на угол Dj или взяв в качестве примера обращение материальной точки относительно этой же оси, рис. 1.5 (точка 0 — начало координат, точка 0¢ — центр окружности, ось y — ось вращения). При вращательном движении вводят понятие — вектор угла поворота Djr , который направлен вдоль оси вращения. Ориентация этого вектора определяется правилом буравчика (рукоятка буравчика вращается вслед за рассматриваемой точкой — рис. 1.5, а направление его поступательного движения задаёт направление вектора Djr ). При векторной форме задания угла поворота, его величина считается небольшой.

Векторная величина w (омега), характеризующая быстроту поворота точки, называется её угловой скоростью:

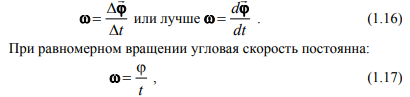
где j — угол поворота за время t. Угол поворота измеряется в радианах (рад), угловая скорость (рад/с).

При равномерном вращении постоянен и модуль линейной скорости |v| (упрощённо просто u). Исходя из того, что радиан соответствует расстоянию по окружности, равному её радиусу имеем:

u = w×R . (1.18)

В более общем плане v = [w,r].

Равномерное вращение характеризуется периодом вращения T, под которым понимают промежуток времени за который рассматриваемая точка поворачивается на угол j = 2p. В результате можем записать

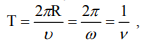
где n — частота вращения, равная числу оборотов в единицу времени. Модуль угловой скорости w часто называют круговой частотой.

РАВНОПЕРЕМЕННОЕ ДВИЖЕНИЕ

Равнопеременное движение точки соответствует условию, когда касательное ускорение (в случае прямолинейного движения полное ускорение) постоянно. Важно понять, что движение с постоянным ускорением может и не быть прямолинейным, например, при невертикальном бросании тела с башни (рис. 1.3) полное ускорение g всегда направлено к центру Земли, если, конечно, отсутствует боковое усилие в процессе его полёта.

В качестве примера равнопеременного движения рассмотрим движение материальной точки в направлении оси x, рис. 1.6.

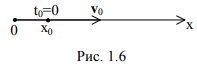
Если при равнопеременном прямолинейном движении направление вектора ускорения a совпадает с направлением вектора начальной скорости v0, то такое движение называется равномерно ускоренным (обычно называют просто — равноускоренным), если — противоположно, то равномерно замедленным (равнозамедленным).

Из определения ускорения имеем:

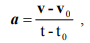
если для удобства анализа возьмём t0=0, то получим

v=v0+at .

В нашем примере (рис. 1.6) u0>0, так как вектор v0 направлен вдоль положительного направления оси x. Если ускорение a совпадает с направлением вектора v0, то a>0, если не совпадает, то a

u=u0±at ,

в этом варианте u — величина скорости материальной точки и a представляет собой модуль её ускорения. С учётом (1.22) координата x может фиксироваться с помощью уравнения

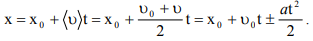
Если направление вектора v0 по оси x имеет два варианта (вдоль и против положительного направления), то выражение (1.23) запишется как

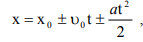
где u0 — модуль вектора начальной скорости. Если в системе уравнений (1.22), (1.23) исключить время, то полу

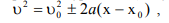
которое при движении в одном направлении имеет вид

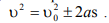
Мы рассмотрели движение материальной точки вдоль одной из осей координат. Это удобно, так как при прямолинейном движении декартову систему координат можно развернуть таким образом, чтобы движение происходило в направлении выбранной оси.

В общем случае, если мы имеем в пространстве векторы, характеризующие движение:

равномерное прямолинейное v=const, r=r0+vt

равноускоренное движение

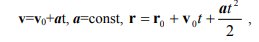
то для построения графиков движения и проведения расчётов (векторную функцию нельзя изобразить в виде графика) осуществляют проекцию векторов на оси координат.

ГРАФИКИ ДВИЖЕНИЯ

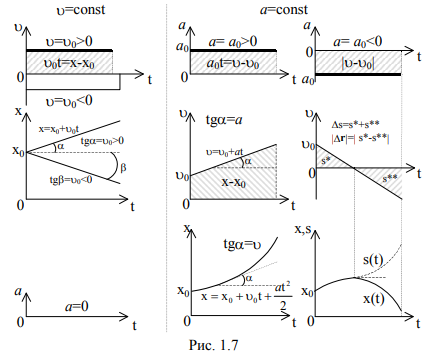
Возьмём за основу вариант движения, показанный на рис. 1.6. Зная аналитические выражения, характеризующие отдельные виды движений (п. 1.3.3) легко получить и их графические представления, рис. 1.7.

На графиках представлены путь s, координата x и проекции векторов v и a на ось x в зависимости от времени для равномерного и равнопеременного движений.

Следует иметь в виду, что площадь под кривой, описывающей зависимость модуля вектора скорости от времени, можно рассматривать как путь, пройденный телом за интервал времени t2-t1=Dt, так как

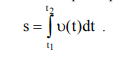
КИНЕМАТИКА В ПРИМЕРАХ

Пример № 1. В чём неточность в определении равномерного прямолинейного движения?

… за равные промежутки времени тело совершает одинаковые перемещения вдоль прямой.

Дело в том, что за определённый промежуток времени, например за 1 час, тело может иметь и одинаковые перемещения, допустим 50 км (на автомобиле), но в первые 30 мин. можно проехать 20 км, а во вторые — 30 км, в целом будет 50 км, движение уже не будет равномерным.

Поэтому важно подчеркнуть, что тело за любые равные промежутки времени имеет одинаковые перемещения или за равные, сколько угодно малые промежутки времени, наблюдаются одинаковые перемещения, то есть v=ávñ=const.

Пример № 2. Каков характер движения материальной точки, показанного на рис. 1.8?

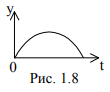
Обычно отвечают, что это движение тела, брошенного под углом к горизонту. В этом случае путается зависимость координаты y=f(t) с уравнением траектории y=f(x). Зависимость, показанная на рис. 1.8 может соответствовать и телу, брошенному вертикально вверх вдоль оси y:

Пример № 3. Дан график проекции скорости при движении вдоль оси x, рис. 1.9. Найти график координаты x(t), пути s(t) и проекции ускорения на ось x – a(t).

Примечание: путь — это скалярная, неотрицательная величина, которая не может уменьшаться.

Пример № 4. С моста высотой h, бросают одновременно два шарика: один — вертикально вверх со скоростью u10, а другой — вертикально вниз со скоростью u20, рис. 1.10. Найти промежуток времени Dt, отделяющий моменты их падения в воду.

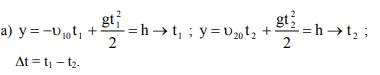
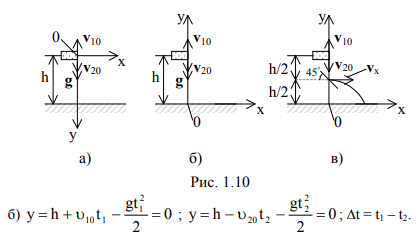
в) На половине высоты моста происходит абсолютно упругий удар, и шарики отскакивают горизонтально. Изменится ли t1 и t2 ? Да, не будет скорости uy после отскока (задержка); x=ux×t .

Пример № 5. С моста высотой h под углом a к горизонту бросают мяч, рис. 1.11. Найти дальность полёта s, если начальная скорость u0.

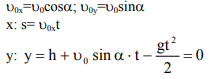
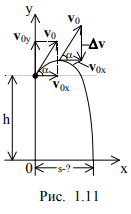
Чему равна uy в верхней точке подъёма?

Ответ: uy=0.

А ускорение?

Ответ: g — везде одинаково.

Найти приращение вектора скорости точки за время от начала полёта до достижения наибольшей высоты подъёма?

|Dv|=u0sina .

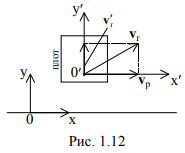
Пример № 6. Человек идёт по плоту перпендикулярно берегу со скоростью vr¢ относительно плота. Скорость течения реки относительно берега (ровные берега) — vр. Найти скорость человека относительно берега.

В данном случае работает закон сложения скоростей: скорость тела относительно неподвижной системы отсчёта равна векторной сумме скорости тела относительно подвижной системы отсчёта и скорости подвижной системы относительно неподвижной, рис. 1.12.

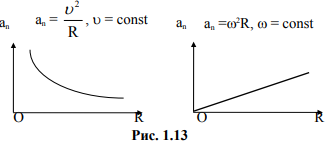
Пример № 7. Изобразить график зависимости центростремительного (нормального) ускорения an от радиуса окружности, по которой движется тело:

В заключение, касаясь единиц измерения физических величин, заметим, что в кинематике (из семи используемых в системе СИ) вводятся: метр (м) — единица длины и секунда (с) — единица времени. Дополнительной единицей Международной системы является радиан — единица плоского угла.

Основными единицами измерения являются семь следующих: метр, килограмм, секунда, ампер, кельвин, кандела (свеча) и моль.

ДИНАМИКА. ОБЩИЕ ЗАМЕЧАНИЯ

Движение тел возникает и изменяется в результате взаимодействия. Взаимодействие может осуществляться как между непосредственно соприкасающимися телами или частицами вещества, так и удаленными друг от друга через так называемое физическое поле. Под физическим полем понимают особую форму материи, которая связывает частицы вещества в единые системы и передает с конечной скоростью действие одних частиц на другие.

К настоящему времени известны четыре класса фундаментальных взаимодействий: гравитационное (r ® ¥), электромагнитное (r ® ¥), сильное (r » 10-15м) и слабое (r » 10-18м).

Мерой механического взаимодействия тел является векторная величина F, которая называется силой. Измерение силы можно проводить статическими и динамическими способами. Первый способ – статический, основан на уравновешивании измеряемой силы с помощью другой, откалиброванной. Второй (динамический) использует основной закон динамики ускоренно движущегося тела.

ЗАКОНЫ НЬЮТОНА

В основе динамики лежат три закона Ньютона, сформулированные в 1687 г. в его знаменитой работе «Математические начала натуральной философии». Рассмотрим последовательно эти законы.

Системы координат можно связывать с различными телами. Особо важный класс тел представляют невзаимодействующие или свободные тела. Свободным называют тело, настолько удаленное от всех остальных, что их воздействие на движение данного тела пренебрежимо мало. Размерами свободных тел часто можно пренебречь, считая их материальными точками. Свяжем с группой одинаково движущихся свободных тел систему координат. В такой системе отсчета, как показывает опыт, все другие свободные тела движутся равномерно и прямолинейно. Таким образом, для свободных тел справедливо утверждение: существуют системы отсчета, в каждой из которых невзаимодействующие тела могут двигаться равномерно и прямолинейно (или, как частный случай такого движения, находиться в состоянии покоя). Это утверждение носит название I закона Ньютона или закона инерции (основные выводы получены еще Г. Галилеем). Системы отсчета, связанные со свободно движущимися телами называют инерциальными системами отсчета. При условии введения меры механического воздействия – силы, этот закон можно сформулировать следующим образом: материальная точка сохраняет состояние покоя или равномерного прямолинейного движения, если на нее не действуют никакие силы или действие сил взаимно скомпенсировано, то есть

Взаимодействие тел, как показывает опыт, вызывает изменение их скоростей

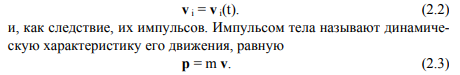
Это векторная величина, которая в каждый момент времени совпадает по направлению с вектором мгновенной скорости. Коэффициент пропорциональности в (2.3) характеризует объект движения и его называют массой тела (измеряется в системе единиц СИ в килограммах – кг).

Таким образом, в процессе воздействия на данную материальную точку других тел ее импульс изменяется. В этом плане в качестве меры взаимодействия тел выбирается физическая величина, которая выражается через скорость изменения импульса и которую в динамическом понимании назвали силой:

Представленное равенство (2.4) носит название II закона Ньютона. Это фундаментальный закон классической физики: скорость изменения импульса материальной точки равна равнодействующей всех приложенных к ней сил. Его можно записать и в другой форме

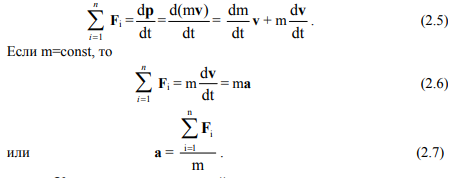
Ускорение материальной точки пропорционально равнодействующей всех приложенных к ней сил, обратно пропорционально ее массе и сонаправлено с равнодействующей сил (II закон Ньютона). Согласно (2.7) сила измеряется в кг×м/с2, эта единица измерения получила название ньютон (Н).

Выражение (2.7) позволяет конкретизировать понятие массы. Из этого уравнения видно, что при одинаковой величине силы, воздействующей на тело, ускорение материальной точки тем меньше, чем больше ее масса. Свойство тел сохранять состояние покоя или равномерного прямолинейного движения называется инертностью (инерцией). Таким образом, материальная точка, получившая меньшее ускорение, будет более инертной, т.е. масса, входящая в формулу II закона Ньютона, характеризует инерцию тела и ее называют инертной массой. Опыт показывает, что с массой также связана способность тел притягиваться друг к другу (гравитационная масса).

Примеры

1. На тело, падающее на поверхность Земли действуют две силы: сила притяжения F (гравитация) и сила сопротивления воздуха FС. Направляя координатную ось вертикально вниз, имеем в проекциях на эту ось уравнение движения (см. уравнение 2.7):

 

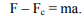
2. Согласно II закону Ньютона (см. 2.4 и 2.5) даже при малой величине равнодействующей силы при длительном воздействии можно сдвинуть с места тела очень большой массы – F D t = D p (автомобиль, стоящий на дороге или вагон, находящийся на ровном железнодорожном пути может сдвинуть один человек). Наоборот, при кратковременном ударе (гашении импульса) можно получить огромное силовое воздействие, часто приводящее даже к разрушению тел.

Рассматривая замкнутую систему из двух материальных точек можно убедиться, что силы их взаимодействия одинаковы по модулю и направлены в противоположные стороны вдоль соединяющей эти точки прямой

F12 = –F21.

Это утверждение носит название III закона Ньютона. Силы F12 и F21 называют силами действия и противодействия.

Пример. Человек, передвигая объемную мебель по полу (шкаф, диван и т.д.) прикладывает к ней определенное усилие, и, в свою очередь, получает противодействие –F21, равное по модулю и направленное противоположно воздействию человека на данный объект. Передвижение человека возможно только из-за наличия третьего объекта взаимодействия – пола, от которого он отталкивается. Важно понять, что силы, возникающие при взаимодействии тел, не могут уравновесить друг друга, так как приложены к разным телам.

Любая система отсчета, движущаяся по отношению к инерциальной системе отсчета (и.с.о) поступательно, равномерно и прямолинейно, является также и.с.о. И.с.о – это абстракция, ибо всегда существуют параллельно элементы криволинейного движения (например, Земля вращается вокруг собственной оси и вокруг Солнца).

Для и.с.о работает принцип относительности, согласно которому все законы физики одинаковы во всех и.с.о. Его частным случаем является принцип относительности Галилея: во всех инерциальных системах отсчета при одинаковых начальных условиях все механические явления протекают одинаково, по одинаковым законам

Если система отсчета движется с ускорением, то в ней не будет выполняться ни I, ни II законы Ньютона. Чтобы I и II законы Ньютона работали в неинерциальных системах отсчета, к телам прикладывают так называемые силы инерции (они не обусловлены взаимодействием тел, к ним не применим III закон Ньютона) – FИНЕРЦ. = –ma.

Обсуждая законы Ньютона, мы пользовались понятием материальной точки, хотя размерами тела пренебречь нельзя по сравнению с размерами других тел. Однако, модель материальной точки часто применима, так как тела движутся во многих случаях только поступательно.

ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ. СИЛА ТЯЖЕСТИ

Этот закон сформулирован И. Ньютоном в 1682 году: две любые материальные точки притягиваются друг к другу с силой, модуль которой прямо пропорционален произведению масс этих точек и обратно пропорционален квадрату расстояния между ними, то есть

Опыты Галилея, показывающие, что все тела в пустоте падают с одинаковым ускорением, позволяют считать mи = mг (современные эксперименты подтверждают это с погрешностью до 10-12), поэтому

 

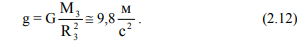
Равенство для всех веществ инертной и гравитационной масс получило название принципа эквивалентности.

Силу mg, с которой Земля притягивает к себе тела называют силой тяжести, точку приложения этой силы – центром тяжести тела.

Все силы, которые мы будем в дальнейшем показывать на чертежах, при отсутствии вращения тела, будут приложены к этой точке.

СИЛЫ УПРУГОСТИ. ЗАКОН ГУКА

Изменение формы или размеров тела называют деформацией. Причина деформации кроется в различных ускорениях у отдельных частей тела.

Силы упругости – это силы, появляющиеся при деформации тела и направленные в сторону восстановления его прежних форм и размеров под прямым углом к деформируемой поверхности.

Упругими называются такие деформации, когда тело полностью восстанавливает свою форму и размеры после снятия внешнего усилия.

Закон Гука: сила упругости, возникающая при действии на тело внешних сил, пропорциональна его деформации и направлена в сторону, противоположную направлению перемещения частиц тела при деформации. В частности

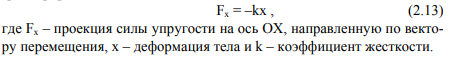
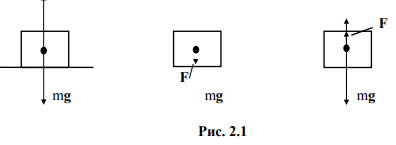
Силу упругости N, возникающую в результате деформации опоры при воздействии на нее внешних сил и действующую на тело, называют силой реакции опоры (рис. 2.1).

 

СИЛА ТРЕНИЯ

Сила сопротивления, появляющаяся на границе раздела двух соприкасающихся тел при их относительном перемещении или попытке перемещения, называется силой трения.

Максимальное значение силы трения, когда еще не наблюдается скольжение одного тела относительно другого, называется силой трения покоя. После того, как начнется относительное перемещение тел, между ними действует так называемая сила трения скольжения, по величине несколько меньшая, чем сила трения покоя. Для инженерных расчетов можно считать силу трения покоя равной силе трения скольжения.

Если составляющая приложенной к телу силы, лежащая в плоскости соприкосновения двух тел не вызывает скольжение, то возникающую силу трения обычно называют неполной силой трения.

При качении одного тела по другому появляется так называемая сила трения качения (в данном курсе не рассматриваем).

Сила трения скольжения пропорциональна силе нормального давления одного тела на другое и приложена к поверхности соприкосновения тел. В соответствии с III законом Ньютона сила нормального давления равна силе реакции опоры N, при этом при скольжении тела

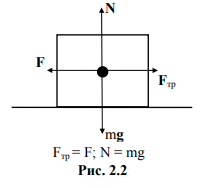
Пример: тело покоится или движется с постоянной скоростью (рис. 2.2).

 

ДВИЖЕНИЕ ТЕЛА ПО ОКРУЖНОСТИ

При равномерном движении тела по окружности, его ускорение равно центростремительному (нормальному) ускорению

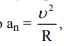
которое всегда направлено по радиусу к центру вращения. Силы, вызывающие вращательное движение тела те же самые, что и в случае прямолинейного движения. II закон Ньютона при этом имеет вид

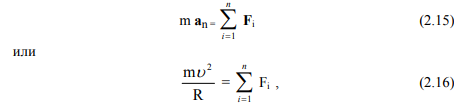
где Fi – проекции сил, приложенных к телу на направление центростремительного ускорения

 

ВЕС ТЕЛА И НЕВЕСОМОСТЬ

Весом тела называют силу, с которой тело вследствие притяжения Земли действует на горизонтальную опору или вертикальный подвес. В соответствии с III законом Ньютона модуль веса тела равен силе реакции опоры или силе натяжения связи.

Необходимо помнить, что вес тела и сила тяжести не одно и то же. Эти силы приложены к разным телам и различие их по абсолютной величине определяется многими причинами. Рассмотрим несколько примеров:

1. Тело находится в лифте, движущемся в вертикальном направлении

 

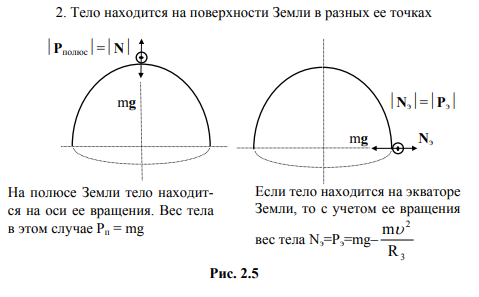
Если тело не действует на опору или подвес, то говорят, что оно находится в состоянии невесомости. В этом случае на тело действует только сила земного притяжения (состояние свободного падения).

В деталях методика решения задач на законы Ньютона будет рассмотрена на практических занятиях. Общая схема решения таких задач выглядит следующим образом:

1. Начертить рисунок в соответствии с условиями задачи.

2. Выполнить анализ взаимодействий тел и на его основе создать чертеж сил, действующих на рассматриваемые тела.

3. Изобразить на рисунке систему отсчета (тело отсчета и связанную с ним систему координат).

4. Записать соотношения по II закону Ньютона для каждого из движущихся тел системы в векторной форме.

5. Записать эти же уравнения в проекциях на оси координат.

6. Решить полученную систему уравнений относительно неизвестных величин и проверить их размерность.

Пример. Определить ускорение, с которым движется тело по горизонтальной поверхности, если известен коэффициент трения m между телом и поверхностью. К телу приложена внешняя сила F, направленная под углом a к горизонтальной поверхности. Масса тела – m (рис. 2.6).