1.1. Основы механики и кинематики

Основы технической механики

Статика и ее основные понятия и определения.

В механике изучаются законы взаимодействия и движения твердых тел.

Механическим движением называется происходящее с течением времени изменение положения точек или тел в пространстве. Частным случаем движения является состояние покоя. Покой всегда имеет относительный характер, так как покоящееся тело рассматривается как неподвиж­ное по отношению к другому телу, которое, в свою очередь, может перемещаться в пространстве.

Абсолютно твердым телом называется тело, когда расстояние между любыми его точками не меняется при действии на него других тел. В статике полагают, что тела абсолютно твердые и их физико-механические свойства не учитывают.

В статике любое тело можно считать материальной точкой, размерами которого в условиях данной задачи можно пренебречь.

Материальной точкой называется точка, имеющая массу.

Свободным называется тело, когда никакие другие тела не препятствуют его перемещению в любом направлении. В противном случае тело называется несвободным.

Сила есть мера механического взаимодействия тел. Она характеризу­ется числовым значением, направлением и точкой приложения. Из этого следует, что сила — величина векторная. Числовое значение силы называется модулем вектора силы. Направление силы есть направление того движения, которое получила бы покоящаяся свободная материальная точка под действием этой силы.

Линия действия силы - это прямая линия, по которой направлен вектор силы.

Единицей измерения силы в системе СИ является Ньютон (Н) -это сила, сообщаемая телу массой 1 кг ускорение 1м/с в направлении действия силы.

Допускаются внесистемные единицы: килограмм-сила (КС, КГ), тонна-сила (ТС), дина.

Между перечисленными единицами силы существуют следующие зависимости:

1Н=105дин=0,102кг.

Графически силу изображают отрезком прямой со стрелкой;

длина отрезка в определенном масштабе равна модулю вектора силы.

Масштаб силы: сколько единиц модуля силы содержится в единице длины ее вектора

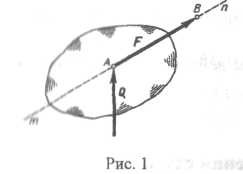
На рис. 1 изображена сила, приложенная в точке А и действующая по линии тп. Вектор силы обозначается, как правило, буквой с черточкой над ней (F), а модуль без черточки (F). Для силы F точка А называется началом, а точка В концом вектора. Нередко удобно изображать вектор силы так, чтобы стрелка, стоящая в конце вектора, упиралась в точку приложения силы (сила Q).

Системой сил называется сово­купность нескольких сил, приложенных к телу, в точке или системе тел и точек.

Система сил, линии действия которых лежат в различных плоскостях, называется пространственной, а в одной плоскости - плоской.

Система сил, с пересекающимися в одной точке линиями действия, называется сходящейся, которая может быть плоской и пространственной.

Различают также систему параллельных сил как частный слу­чай произвольно расположенных сил, в которых линии действия сил не схо­жи в одной точке.

Они также могут быть плоскими и пространственными.

В статике решаются следующие три основные задачи:

1. Приведение данной системы сил к другой, более простой, статистически эквивалентной системе;

2. Нахождение условий равновесия данной системы сил;

3.Определение сил взаимодействия между материальными объектами.

Аксиомы статики

В основе статики лежит ряд основных положений, полученных в ре­зультате наблюдений, опыта и практической деятельности людей. На ос­новании этих положений, называемых аксиомами статики, путем строгих математических доказательств делаются все последующие выводы.

1 аксиома статики, получившая название аксиомы инерции, за­ключается в следующем:

Аксиома 1. Изолированная материальная точка находится в состоя­нии покоя или движется равномерно и прямолинейно.

Согласно этой аксиоме, материальная точка может двигаться равно­мерно и прямолинейно без приложенной к ней силы (по инерции). Изме­нить состояние покоя или равномерного прямолинейного движения мате­риальной точки может только сила.

Упомянутые два состояния точки объединяются в общем понятии "равновесие".

Аксиома 2. Две силы, приложенные к твердому телу, взаимно урав­новешиваются только тогда, когда они равны по величине и направлены по одной прямой в противоположные стороны (рис. 1.1).

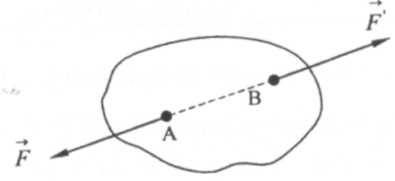 Из этой аксиомы и рис. 1.1. следует, что при равновесии рассмат­риваемого тела F = F Рис. 1.1

Аксиома 3. Две силы, приложенные к твердому телу в одной точке, имеют равнодействующую, приложенную в этой же точке и изображаются диагональю параллелограмма, построенного на этих силах, как на сторонах.

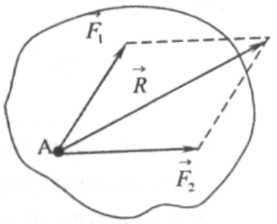 На рис 1.2 показана равнодействующая R двух сил F1 и F2, при­ложенных к твердому телу в точке А. Операция замены системы сил её равнодействующей называется сложени­ем данной системы сил.

Мы видим, что сложение двух сил, приложенных к твердому телу в одной точке, подчиняется правилу векторного сложения, чем подтверждается вы­сказанное предположение о том, что сила есть вектор.

Таким образом, равнодействующая двух сил, приложенных к твердому телу в одной точке, равна их векторной сумме, т.е. ¯R = ¯F1+¯F2. (1.1)

Аксиома 4. Присоединение или отбрасывание взаимно уравновеши­вающихся сил не изменяет действия данной системы сил на твердое тело.

Например, если Q=Q, то системы сил, показанные на рис. 1.3, ста­тически эквивалентны, так как на основании аксиомы 2 силы Q и Q/ вза­имно уравновешиваются и, следовательно, в силу аксиомы 4, их можно присоединить или отбросить.

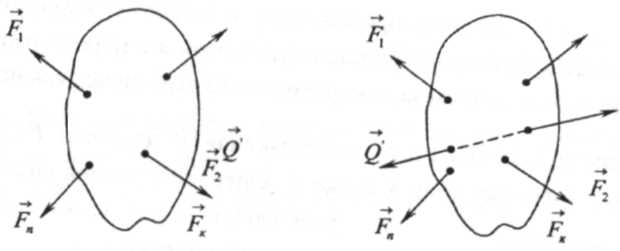
Рис. 1.3

Аксиома 5. Если каждая из двух систем статически эквивалентна одной и той же третьей системе, то они статически эквивалентны между собой. Понятно, что если система сил А статически эквивалентна системе С, и в то же время система В статически эквивалентна системе С, то и сис­темы А и В статически эквивалентны одна другой.

Из приведенных аксиом вытекают следующие следствия.

Следствие 1. Не изменяя действия силы на твердое тело, можно пе­реносить её точку приложения вдоль линии действия на любую точку тела.

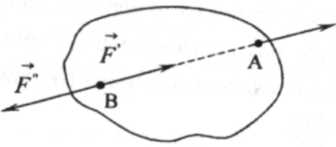
Рис. 1.4

В самом деле, три одинаковые по модулю силы F , F / и —► F ? / (рис. 1.4), направленные вдоль прямой, проходящие через точки А и В, статически эквивалентны, с одной стороны, силе F, так как силы F и F" взаимно уравновешиваются, и с другой стороны, силе и F , так как уравновешиваются силы F и F'/ . Следовательно, статически эквивалентны силы F и F"', т.е. точку А приложения силы F можно переносить вдоль её линии в любую точку В твердого тела.

Такие векторы, которые по их физическому смыслу можно перено­сить вдоль прямых, по которым они направлены, называются скользящими векторами.

Следовательно, сила есть вектор скользящий.

Следствие 2. Сила ¯R (рис. 1.5) равная по модулю равнодействующей ¯R и направленная по одной с ней прямой в противоположную сторо­ну, уравновешивает данную систему сил.

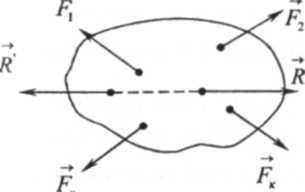 Поскольку сила R/ уравновешивает равнодействующую R, то она уравновешивает и статистически экви­валентную ей систему сил. F1 F2 ….Fn

Шестая аксиома, называемая аксиомой действия и противодействия, заключается в следующем:

Аксиома 6. Силы взаимодействия любых двух материальных объек­тов всегда равны по величине и направлены по одной прямой в противопо­ложные стороны.

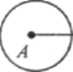 ¯ F¯ F?¯  Эта аксиома, сформулированная Ньютоном, означает, что если объект А (рис. 1.6) действу­ет на объект В и это действие выражается силой F , то объект В оказывает объекту А противодействие, выраженное силой F/ , причем F = - F'.

Таким образом, всякой силе, приложенной к некоторому материаль­ному объекту, соответствует равная ей по модулю и прямо противополож­ная по направлению сила, приложенная к другому объекту, взаимодействующему с данным. Подчеркнем, что силы действия и противодействия не уравновешивают друг друга, так как они приложены к различным объектам.

Седьмая аксиома называется аксиомой отвердения. Она заключается в следующем:

Аксиома 7. Если нетвердое тело находится в равновесии под дейст­вием приложенных к нему сил, то равновесие его не нарушается при его отвердении.

Из этой аксиомы следует, что если нетвердое тело находится в равновесии под действием прило­женных к нему сил, то под действием этой же системы сил будет находиться в равновесии и Рис. 1.7 соответствующее абсолютно твердое тело.

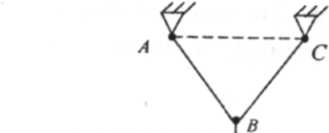 Например, если нить ABC (рис. 1.7), закрепленная в точках А и С, находится в равновесии под действием приложенной к ней вертикальной

силы F, то под действием этой же силы будет находиться в равновесии и абсолютно твердое тело, имеющее такую же форму. Обратное заключение сделать нельзя, т.е. из того, что под действием некоторой системы сил на­ходится в равновесии абсолютно твердое тело, вовсе не следует, что под действием этой же системы сил будет находиться в равновесии и любое нетвердое тело.

Например, если к нити, показанной на рис. 1.7 приложить в. точке В силу, направленную по вертикали вверх, то она не будет находиться в рав­новесии, тогда как соответствующее абсолютное твердое тело и в этом случае будет находиться в равновесии.

Из этого следует, что вместо равновесия реально сущест­вующих тел, можно рассматривать равновесие соответствующих абсолют­но твердых тел.

Этими аксиомами и следствиями из них мы будем пользоваться при изложении последующих тем статики, в которых рассматриваются различ­ные виды систем сил, приложенных к материальному объекту.

Простейшей из таких систем является система сходящихся сил.

 Система сходящихся сил.

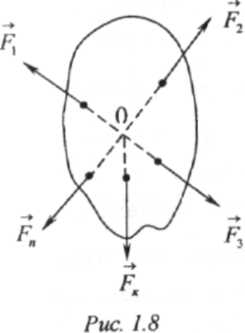
Ранее были рассмотрены аксиомы статики и их основные определения. Теперь перейдем к изу­чению простейшей системы сил. Такой системой является система сходящихся сил, т.е. таких сил, линии которых пересекаются в одной точке (рис. 1.8).Если линии действия всех сил такой системы расположены в одной плоскости, то система назы­вается плоской системой сходящихся сил. В про­тивном случае эта система называется простран­ственной системой сходящихся сил.

 Приведение системы сходящихся сил к простейшему виду

а) Геометрический метод сложения сходящихся сил .

Термин "сложить систему сил" означает - найти её равнодействую­щую. Задачи о сложении и равновесии сходящих­ся сил впервые решены Вариньоном. Начнем решение с поставленной задачи со случая сложения двух сходящихся сил. Пусть в точках А и В (рис. 1.9) к твердому телу приложе­ны две силы F1 и F2, линии действия которых пе­ресекаются в точке О.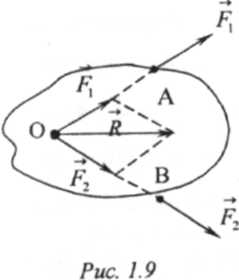 

Поскольку сила является вектором скользящим, то перенося каждую из данных сил F1и F2 вдоль их действия в точку О, получим две силы, приложенные к твердому телу в одной точке О. Сложив их, на основании аксиомы 3, получим равнодействующую А, приложен­ную в этой точке и изображенную диагональю параллелограмма, постро­енного на этих силах, как на сторонах. Такой способ сложения двух схо­дящихся сил называется правилом параллелограмма сил.

Эта же задача также может быть решена с помощью правила треугольника сил, заключающего­ся в следующем (рис. 1.10). -

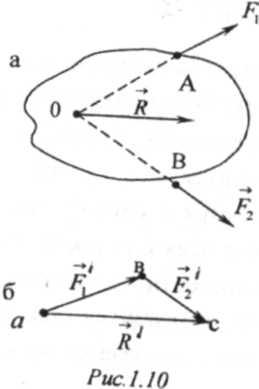
Из произвольной точки а (рис. 1.10б) проведем вектор f/=f, и из конца его b вектор f1=F2. Соединив точку а с концом вектора f2, получим вектор r', равный рав­нодействующей r данных сил. Последняя сила приложена в точке 0 пересечения линий действия данных сил f, и f2.

Теперь допустим, что требуется сложить систему сходя­щихся сил f1, f2 f,3 приложенных к твердому телу в различных его точках a1, а2, ...ап (рис. 1.11).

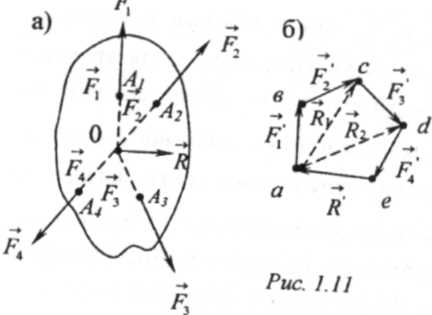
Перенеся все силы вдоль их линий действия в общую их точку пере­сечения, получим систему сил приложенных к данному телу в одной точке 0. Для сложения сил воспользуемся методом последовательного их сложе­ния.

Сложим сначала силы f1 и f2, использовав правило треугольника сил. Для этого из произвольной точки а (рис. 1.11б) проведем последовательно векторы F1f2 , равные соответственно векторам f1 и f2. Равнодействующая этих сил равна век­тору r', проведенному из точки а в конец с вектора f2 , и приложена в точке 0 пересечения линий дей­ствия данных сил (рис. 1.11а), причем r, =F1 +f2 . На рис. 1.11 б вектор R, показан пунктиром. Теперь, найденную равнодействующую r, сложим со следующей силой f3. Для этого из конца с вектора r1 проведем вектор f2 =f3. Тогда вектор R2 (см. пунктир на рис. 1.116), проведенный из точки а в конце d вектора F3, будет равен равнодействующей сил R, и F3, т.е. трех сил F 1F2, F3, причем R 2=R1 +F3,=Ft +F2 +F3. Приложена эта равнодействую­щая также в точке 0 (на рис. 1.11а) равнодействующие R2 и R1, не показа­ны. Аналогично складывая равнодействующую R2 последовательно со всеми остальными силами данной системы, получим равнодействующую r всех данных сил, приложенную в точке 0 и равную r = R/ =F1+F2'+F3'+...+ Fп' =ΣFк,

где R' - вектор, проведенный из точки а в конец е последнего из векторов, построенных на рис. 1.116.

Учтя, что Fk=Fk (к=1,2,...п), окончательно получим r = ΣFк. .

Сумма, стоящая в правой части этого равенства, называется векторной суммой сил.

Как нетрудно видеть, для построения вектора r равнодействующей системы сходящихся сил достаточно, начиная от произвольной точки а провести последовательно один за другим векторы f1,f2,...,fп, равные со­ответственно векторам данной системы сил F, ,F2 ,.. fп, из точки а про­вести вектор r в конец е последнего из проведенных векторов и затем перенести его параллельно в точку 0 пересечения линий действия данных сил. Многоугольник abcde называется многоугольником сил, а такой способ сложения системы сходящихся сил получил название правила многоуголь­ника. Вектор r , направленный противоположно всем остальным сторо­нам многоугольника adcde при обходе его периметра, называется замы­кающей стороной многоугольника сил.

Таким образом, равнодействующая системы сходящихся сил равна замыкающей стороне многоугольника сил, построенного на данных силах, как на сторонах, или векторной сумме этих сил, и приложена в точке пере­сечения их линий действия.

Заметим, что описанный способ применим не только для сложения плоской системы сходящихся сил. Им можно также пользоваться и при сложении сходящихся сил, не лежащих в одной плоскости, хотя в послед­нем случае применение его очень неудобно, так как трудно изобразить на плоскости пространственный многоугольник сил.

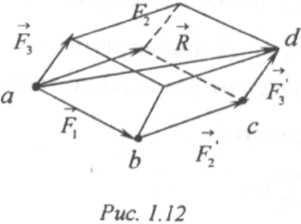
Особого внимания заслуживает сложение трех сходящихся сил, ли­нии действия которых не лежат в одной плоскости. Пусть дана пространственная система трех сходящихся сил F1, F2, F3, (рис. 1.12). Построим на этих силах пространственный многоугольник сил abсd (точка а этого многоугольника совмещена с точкой приложения сил данной системы).

Его замыкающая сторона ad = R равна по величине и направлению равнодействующей данных сил. Достроив этот многоугольник до параллелограмма, как это показано на рисунке, убедим­ся, что вектор равнодействующей R изображается его диагональю, а векторы данных сил F1, F2 и F3 - ребрами, исходящими из той же верши­ны d, из которой проведен вектор r .

Таким образом, приходим к выводу, что равнодействующая трех сходящихся сил, линии действия которых не лежат в одной плоскости, изображается диагональю параллелепипеда, по­строенного на данных силах, как на ребрах, исходящих из общей вершины.

б) Векторное условие равновесия системы сходящихся сил

Пусть r - равнодействующая системы сходящихся сил F1, F2, ..,Fп-1, (рис. 1.13).

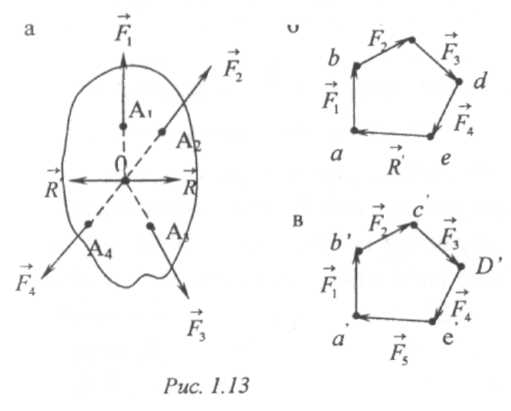
Поскольку сила R ', равная по модулю равнодействующей R и направленная по той же прямой в противоположную сторону, уравновешивает данную систему сил, то, присоединив к данной системе сил Fп = r (на рис. 1.13 силу F5) , мы получим взаимно уравновешенную систему сил F1, F2 , .., Fп (на рис. 1.13 систему F1 F2, .., Fп).

Если теперь вектор Fn присоединить к ломаной кривой abсde, то конец его совпадает с началом а вектора первой силы F, (рис. 1.1 Зв). Многоугольник сил abсdea, стороны которого направлены при обходе вдоль его периметра в одном и том же направлении, называется замкнутым. Равнодействующая такой системы сил равна нулю.

Следовательно, если система сходящихся сил вза­имно уравновешивается, то соответствующий много­угольник сил замкнут и рав­нодействующая или вектор­ная сумма сил равна 0.

Таким образом, необходимым усло­вием равновесия системы сходящихся сил является равенство 0 векторной суммы данных сил. Это условие является также и достаточным.

В самом деле, если дана система сходящихся сил F1, F2, .., Fп, век­торная сумма которых равна нулю (рис. 1.13в), то, заменив силы F,, F2, .., Fп-1 , их равнодействующей

R= -Fп приложенной в точке 0 (рис. 1.13а), будем иметь две равные и противоположно направленные по одной пря­мой силы R и r =F„, которые, на основании аксиомы 2, взаимно урав­новешиваются. Следовательно, уравновешивается и система сил F1, F2, .., Fп.

Та­ким образом, векторным условием равновесия системы сходящихся сил является векторное равенство: ΣFt=0, что означает, что многоугольник сил, построенный на силах данной систе­мы, должен быть замкнутым.

 Разложение силы на составляющие, приложенные в её точке приложения

Теперь решим обратную задачу. Пусть задана сила¯F, приложенная в некоторой точке А. Требуется разложить её на составляющие, приложен­ные в этой же точке.

Рассмотрим сначала случай разложения силы F на две составляю­щие F1 и F2 (рис. 1.14). Эта задача сводится к построению параллелограм­ма, диагональю которого изображался бы вектор данной силы. Таких паралле­лограммов можно построить бесчислен­ное множество. Следовательно, постав­ленная задача является многозначной. Чтобы сделать её однозначной, необхо­димо задать дополнительные условия.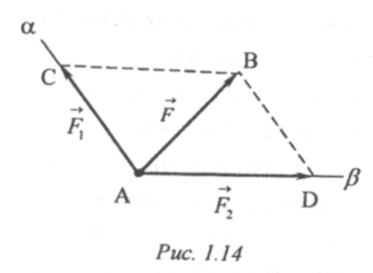  

Наиболее часто встречается задача о разложении силы на две составляющие, приложенные в её точке приложения, по заданным линиям действия иско­мых составляющих.

Пусть силу ¯F, приложенную в точке А (рис. 1.14), требуется разло­жить на две составляющие, приложенные в этой же точке и направленные по заданным прямым Аа и Аβ. Для решения этой задачи достаточно из конца В вектора F провести прямые ВД и ВС, параллельные соответст­венно прямым Аа и Аβ Тогда стороны АС и AD построенного таким обра­зом параллелограмма ABCD изобразят векторы искомых составляющих F1 и F2.

Для разложения силы на две составляющие, приложенные в её точке приложения, могут быть также заданы величины составляющих сил или величина и линия действия одной из них и, наконец, величина одной и ли­ния другой. Во всех этих случаях задача решается путем геометрического построения параллелограмма сил. Предлагается самостоятельно рассмот­реть все эти случаи и выяснить, при каких условиях каждая из этих задач является однозначной, двузначной или не имеет решений.

Рассмотрим теперь случай разложения силы на три некомпланарные составляющие, приложенные в её же точке приложения. Эта задача сво­дится к построению параллелепипеда, диагональю которого изображался бы вектор данной силы, и в общем случае также является многозначной. Для того чтобы сделать её однозначной, необходимо задать дополнитель­ные условия. Наиболее важным является случай разложения силы на три некомпланарные составляющие, приложенные в одной с ней точке, по за­данным линиям действия всех трех составляющих.

Основы кинематики

Кинематика - часть теоретической механики, в которой изучаются механические движения материальных тел без учета их масс и действующих на них сил движения. Кинематика основана на геометрических представле­ниях.

Кинематика изучает движение различных объектов с геометриче­ской точки зрения, т.е. независимо от сил, его вызывающих. В кинематике нас будет интересовать лишь сам факт движения и его характер: траекто­рии отдельных точек объекта, их перемещения в зависимости от времени, их скорости и ускорения, а также зависимости между параметрами движе­ния. С этой точки зрения кинематика является геометрией четырех изме­рений, где четверым измерением является время. Статика и кинематика представляют независимые друг от друга разделы геометрической механи­ки.

В задачи кинематики входит:

а) определение законов движения рас­сматриваемого объекта,

б) определение кинематических параметров (ско­ростей, ускорений) точек этого объекта,

в) определение кинематических параметров (угловой скорости, углового ускорения) твердого тела.

Простейшим геометрическим объектом является геометрическая точка.

Для изучения движения того или иного объекта, надо уметь опреде­лять его положение относительно некоторого движущего тела, называемо­го телом отсчета (рис. 2.1).

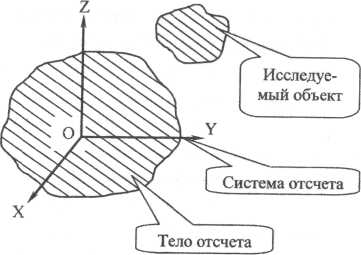
Рис. 2.1

С этим телом неизменно связывается какая-либо координатная сис­тема O x y z, которая называется системой отсчета. При исследовании дви­жения объекта система отсчета условно считается неподвижной, хотя она и движется вместе с телом отсчета. Поскольку движение всякого объекта происходит во времени, то для изучения движения этого объекта необхо­димо вести отсчет времени. За начало отсчета времени принимается неко­торый начальный момент, для которого время считается равным нулю (t-= О). Всякий данный момент времени (момент t ) определяется числом се­кунд, прошедших от начального момента до данного. Момент времени считается положительным, если он следует за начальным моментом, и от­рицательным, если он предшествует начальному. Число секунд, отделяю­щих два последовательных момента времени t 1 и t2, называется промежут­ком времени

Δt = t2 – t1).

Механическое движение происходит в пространстве и во времени. Пространство рассматривается как трехмерное; все свойства его подчиняют­ся системе аксиом и теорем эвклидовой геометрии. Время полагают ни с чем не связанным и протекающим равномерно. Однако современное развитие физики привело к иным представлениям о пространстве и времени. Это дока­зал великий ученый XX века Альберт Эйнштейн, создав теорию относитель­ности, суть которой заключается в том, что пространство и время зависят от скорости движения. Эта зависимость практически не обнаруживается при сравнительно малых скоростях движения и установленные в механике пред­ставления о пространстве и времени сохраняют силу. Но при скоростях, близких к скорости света, которая считается в вакууме постоянной (300000 км/с), представления являются неточными. При измерении времени различают промежуток или отрезок времени и начальный момент времени. Промежуток времени - это время, проте­кающее между двумя фиксированными событиями. Начальным момен­том называется время, с которого начинается отсчет.

Траекторией точки называется кривая, которую описывает точка при движении в пространстве относительно выбранной системы отсчета. Траектория бывает прямолинейная и криволинейная. Движение точки в пространстве определяется скоростью, характеризующей быстроту и направление движения точки в данный момент времени.

В зависимости от скорости движение точки может быть равномерным, когда скорость постоянная по величине и направлению, и неравном

Cкорость и ускорение точки являются векторными величинами.

При изучении движения точки различают два понятия: расстояние и пройденный путь. Расстояние определяет положение точки на ее траекто­рии и отсчитывается от некоторого начала отсчета. Оно является алгебраической величиной, так как в зависимости от положения точки относительно начала отсчета и принятого направления оси расстояний оно может быть положительным и отрицательным.

Пройденный путь всегда определяется положительным числом.

В общем случае движение точки может начинаться из некоторого произвольного положения на траектории. В связи с этим для определения исходного положения точки вводится понятие начального расстояния. При движении точки в одном направлении расстояние и путь могут отличаться только на какую-то постоянную величину, равную начальному расстоянию, Sp =S + S0,

Где Sp - расстояние точки от начала отсчета;

S - пройденный путь;

So- начальное расстояние.

Начальное расстояние может быть выражено как положительной, так и отрицательной величиной.

 Переменный вектор и его годограф

Пусть некоторый вектор А с течением времени изменяет, в общем случае, как свою величину, так и направление. Такой вектор на­зывается переменным. Говорят, что он является векторной функцией вре­мени. Математически это записывается следующим образом: A =f(t). (2.1)

Функция f(t). называется векторной функцией времени.

В частных случаях вектор А может изменять только свою величину, только направление или сохранять неизменными как величину, так и на­правление. В последнем случае он называется постоянным вектором. Это записывается так: А = const. (2.2)

Пусть переменный вектор А (рис. 2.2), начало которого ос­тается в неизменной точке О, а конец занимает в данный момент t некото­рое положение В. Допустим, что в последовательные моменты времени t.1 t2i ts t4, ... этот вектор принимает значения А1. А2, А3, А4, ..., а конец его занимает соответст­венно положения В1, В2, Вз, В4, ...

Линия В В,В2В3В4..., описываемая концом переменного вектора при неизменном его начале О, называ­ется годографом этого вектора.

Понятно, что если вектор изменяет только свое направле­ние, оставаясь в одной и той же плоскости, то его годографом является окружность.

Если же вектор изменяет только величину, то его годограф представляет прямую, по которой он направлен.

Основные кинематические способы определения движения точки

Определить движение точки значит установить закон, которому под­чиняется ее движение, и который позволил бы найти положение точки в пространстве относительно выбранной системы отсчета в любой момент времени. Существует три основных кинематических способа определения движения точки:

векторный, координатный, естественный.

.Векторный способ

Пусть точка М (рис. 2.3), движение которой подлежит определению, двигаясь в пространстве относительно некоторой системы отсчета O x y z, описывает траекторию АВ.

Из какой-нибудь точки, неизменно связанной с этой системой отсчета, напри­мер, из начала координат О, проведем в точку М радиус-вектор r. Понятно, что при движении точки М вектор r, в общем слу­чае, непрерывно изменяет как свою вели­чину (модуль), так и направление. Следо­вательно, он является векторной функцией времени , т.е. r = f(t) (2.3)

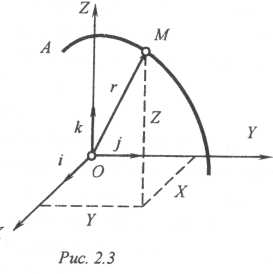
Это векторное равенство выражает закон движения точки М и называется векторным уравнением ее движения. Оно позволяет для любого момента времени построить вектор r (например, по его проекциям на координатные оси) и, следовательно, найти положение точки М относительно выбранной системы отсчета. Траектория точки М представляет собой годограф ее радиуса-вектора r. Функция (2.3) должна быть непрерывной, однозначной и дважды дифференцируемой.

 Координатный способ

Известно, что положение точки в пространстве однозначно опреде­ляется тремя ее координатами: х, у, z относительно выбранной системы координат x O y z (рис. 2.3). При движении точки по траектории, в общем слу­чае, непрерывно изменяются с течением времени все три ее координаты. Таким образом, движение точки описывается уравнениями:

X=f1 (t), У'= f2 (t). Z=f3 (t). (2-4)

Подставив в эти уравнения вместо t любое значение, можно найти положение точки в пространстве в соответствующий момент времени. Следовательно, уравнения (2.4) определяют движение точки относительно выбранной системы отсчета. Эти уравнения называются уравнениями движения точки в координатной форме. Функции (2.4) должны быть не­прерывными, однозначными и, как это будет показано ниже, дифференци­руемыми, по крайней мере, дважды.

Если точка совершает плоское движение, т.е. движется в одной плоскости, то, совместив с плоскостью ее движения одну из координатных плоскостей, например, плоскость х О у, мы обратим в тождество третье уравнение системы (2.4). Таким образом, плоское движение точки определяется двумя уравнениями этой системы. Прямолинейное движение точки определяется одним из этих уравнений, т.к. направив одну из координатных осей вдоль траектории точки, можно обратить в тождества два уравнения системы (2.4).

 Естественный способ

Пусть некоторая точка, совершая движение по траектории KL (рис. 2.4) в момент t занимает положение М. Если точка М движется относительно выбранного тела отсчета, то траектория KL неизменно связана с этим телом. Будем считать, что траектория точки М нам задана. Возьмем на этой траектории неизменно связанную с ней точку А (а сле­довательно, и с телом отсчета).

Т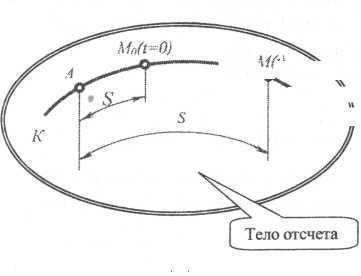 огда положение рассматриваемой точки М на ее траектории будет определено, если задана ее дуговая координата S, отсчитывается вдоль траектории от точки А, называемой началом дуговых координат. Ду­говая координата является величиной алгебраической. Она может быть по­ложительной или отрицательной в зависимости от того, с какой стороны от точки А расположена точка М. Правило знаков для дуговой координаты должно быть выбрано предварительно.

Не следует дуговую координату точки смешивать с длиной пройден­ного ей пути. Пройденный путь всегда положителен и при движении точки всегда возрастает, независимо от направления движения.

Дуговая координата S при движении точки, в общем случае, непре­рывно изменяется с течением времени. Она является непрерывной, однозначной и дважды дифференцируемой функ­цией времени, т.е. S= f (t). (2.5)

Уравнение такого вида определяет движение точки по ее траектории, т.к. подставив в него любое значение времени t, можно определить соответст­вующее алгебраическое значение дуговой координаты S и, таким образом, определяется положение точки на ее траектории в соответствующий момент времени. В этом случае системой отсчета является сама траектория вместе с началом А дуговых координат. Уравнение (2.5) называется уравнением движения точки по ее траектории или уравнением ее движения в естест­венной форме. Заметим, что это уравнение определяет движение точки только в том случае, если задана ее траектория, выбрано начало дуговых координат и правило знаков для дуговой координаты.

Положение М0 занимаемой точкой М в начальный момент, называет­ся начальным ее положением. Дуговая координата So начального положе­ния точки называется начальной дуговой координатой. Она определяется из уравнения (2.5) подстановкой в него t = 0, т.е.

So =f(0). (2.6)

2.3. Частные случаи движения точки

Равномерным называется такое движение, при котором проекция скорости на касательную к траектории постоянна, т.е. V, = const и, следо вательно, ат=0.

Поэтому, а = ап = V 2 / p, т.е. при равномерном криволинейном движении точки полное ускорение равно нормальному. Скорость же при таком движении, оставаясь постоянной по величине, изменяет лишь свое направление. Отсюда следует, что нормальное ускорение характеризует быстроту изменения скорости по направлению.

Движение точки называется переменным, если величина ее скорости изменяется с течением времени. Если при этом величина скорости увели­чивается, то движение называется ускоренным, если уменьшается - замед­ленным. Поскольку точка совершает прямолинейное движение, то в любой точке ее траектории р = оо и, следовательно, ап = 0.

Таким образом, а = ап= V 2 / p т.е. полное ускорение равно тангенциальному. Скорость же при таком движении изменяет лишь свою величину. Отсюда следует, что тангенциальное ускорение характеризует быстроту изменения величины скорости.

При равномерном прямолинейном движении скорость точки не изме­няется ни по величине, ни по направлению.

Равнопеременным движение точки называется такое движение, при котором ее тангенциальное ускорение постоянно, т.е. ат = const.

Динамика поступательного и вращательного движения

Простейшими видами движения твердого тела являются по­ступательное движение и вращение вокруг неподвижной оси. Под твердым телом в кинематике, как и в статике, понимается абсолютно твердое тело.

Рассмотрим основные свойства и зависимости между кинематически­ми параметрами поступательного и вращательного движений твердого те­ла. Заметим, что поступательное или вращательное движение может со­вершать только твердое тело.

Установим взаимосвязь между кинематическими параметрами вра­щательного движения твердого тела вокруг неподвижной оси и движения точки, принадлежащей этому телу. Важное значение здесь имеет передача вращательного движения от одного вала машины к другому. В этом разделе мы выведем зависимость между угловыми скоростями двух валов при передаче вращательного движения от одного к другому. Здесь же мы ознакомимся с двумя новыми векторами - с вектором угловой скорости и вектором углового ускорения твердого тела, вращающегося вокруг неподвижной оси. С помощью этих векторов мы выведем векторные формулы скорости и ускорения точки, принадле­жащей вращающемуся твердому телу, которые будем впоследствии ис­пользовать как в кинематике, так и в динамике.

 Поступательное движение твердого тела

а) Определение и классификация поступательного движения

Поступательным движением твердого те­ла называется такое его движение, при котором любая прямая, неизменно связанная с телом, за все время его движения остается параллельной своему начальному положению. Поступательное движение совершает, например, вагон, движу­щийся по прямолинейному участку пути.

В ка­честве второго примера поступательного движе­ния можно привести движение спарника АВ (рис. 2.5), соединенного шарнирно с концами двух равных по длине кривошипов О1А и О2В, вращающихся в одинаковых направлениях вокруг перпендику­лярных к ним параллельных между собой осей О1 и О2, отстоящих друг от друга на расстоянии, равном длине спарника. Описанный механизм назы­вается шарнирным параллелограммом. При любом положении этого меха­низма сохраняется параллельность между прямой, проходящей через цен­тры шарниров A и В и неподвижной прямой Ot O2. Таким образом, любая прямая CD, неизменно связанная со спарником и, следовательно, обра­зующая с прямой АВ постоянный угол а, образует такой же постоянный по величине угол и с параллельной ей неподвижной прямой О1,О2. Отсюда следует, что за все время движения спарника упомянутая прямая остается параллельной своему начальному положению, т. е. спарник движется по­ступательно. Если при поступательном движении твердого тела все его точки движутся прямолинейно, то такое поступательное движение называется прямолинейным. В противном случае поступательное движение называется криволинейным.

Например, прямолинейное поступательное движение совершает ва­гон, движущийся по прямолинейному участку пути или поршень, движу­щийся в цилиндре двигателя. Спарник АВ, показанный на рис. 2.5, совер­шает криволинейное поступательное движение, так как точки его описы­вают траектории, например, точки А u В движутся по окружностям одина­кового радиуса с центрами в точках О1 и О 2.

Если при поступательном движении твердого тела все его точки пе­ремещаются в плоскостях, параллельных некоторой неподвижной плоско­сти, то такое движение тела называется плоским поступательным. Плос­кое поступательное движение совершает, например, спарник, показанный на рис. 2..5, так как все его точки перемещаются в плоскостях, параллель­ных неподвижной плоскости, проведенной перпендикулярно к осям О1 и О2 вращения кривошипов. Траектории всех точек твердого тела, совер­шающего плоское поступательное движение, расположены в параллельных плоскостях и, следовательно, представляют собой плоские линии. Понят­но, что прямолинейное поступательное движение твердого тела является частным случаем плоского поступательного движения.

Если все точки поступательно движущегося твердого тела описыва­ют пространственные кривые, то такое движение тела называется про­странственным поступательным.

б) Теорема о траекториях, скоростях и ускорениях точек твердого тела при поступательном движении

Прежде чем сформулировать эту теорему, напомним о следующих определениях, известных из элементарного курса геометрии.

Определение 1. Две фигуры называются конгруэнтными, если при наложении одной из них на другую они совмещаются всеми своими точ­ками.

Определение 2. Точки двух конгруэнтных фигур, совмещающиеся друг с другом при их наложении, называются соответствующими точками.

Определение 3. Две конгруэнтные фигуры называются смещенными относительно друг друга параллельно, если их соответствующие точки смещены относительно друг друга по параллельным прямым на одинако­вые расстояния.

Теперь сформулируем следующую теорему.

Теорема 1. Все точки поступательно движущегося твердого тела описывают конгруэнтные параллельно смещенные траектории и имеют в любой момент равные векторы скорости и равные векторы ускорения.

Пусть некоторое твердое тело (рис. 2.6) совершает поступательное движение относительно системы отсчета O x y z. Возьмем две произвольные

его точки А и В и докажем, что они дви­жутся по конгруэнтным параллельно сме­щенным траекториям, имея в любой мо­мент времени равные векторы скорости Vа и Vв и равные векторы ускорения аА и аВ , т.е.

V A =VB и аА =а В

Для доказательства проведем в точки А и В радиусы-векторы rА и rв из на­чала координат О. Проведем также вектор ВА = r. Этот вектор постоянен по величине, так как рассматриваемое тело является абсолютно твердым и, следовательно, расстояние между точками А и В при его движении остает­ся неизменным.

Направление этого вектора также не изменяется, так как, согласно условию, тело движется поступательно, и, поэтому, прямая, про­ходящая через точки А и В, перемещается параллельно своему начальному положению.

Таким образом, вектор r постоянен, т. е. r = const. (2.7)

Следовательно, траекторию точки В можно совместить всеми ее точ­ками с соответствующими точками траектории точки А путем параллель­ного переноса их в направлении вектора r на одинаковые расстояния, рав­ные длине отрезка АВ, чем и доказана первая часть сформулированной теоремы. Из векторного треугольника ОBА замечаем, что гА = гв + г . (2.8)

в) Уравнения поступательного движения твердого тела Теперь мы знаем, что все точки поступательно движущегося твердо­го тела совершают одинаковые движения: по конгруэнтным параллельно смещенным траекториям, с одинаковыми по величине и направлению ско­ростями и ускорениями. Одинаковые для всех точек тела траектории, ско­рости и ускорения называются соответственно траекторией, скоростью и ускорением твердого тела. Отсюда следует, что для исследования поступа­тельного движения твердого тела достаточно исследовать движение какой-либо одной его точки, так как все остальные его точки совершают такие же движения. Эта точка называется полюсом. За полюс может быть принята любая точка данного тела. Например, все точки спарника АВ, показанного на рис. 2.5, движутся по окружности одинакового радиуса, равного длине кривошипов О,А и О2В, а их скорости и ускорения равны по величине ско­ростям и ускорениям точек А и В и одинаковы с ними по направлению. Та­ким образом, в этом примере за полюс можно принять точку А или В.

Движение полюса может быть определено любым из способов, описанных в предыдущей теме: векторным, координатным или естественным.

Например, если принять за полюс точку В (рис. 2.6), то движение его мож­но определить следующим векторным уравнением:

rB=fB(t) (2.11)

Из векторной зависимости (2.8) замечаем, что векторное уравнение движения любой другой точки данного тела отличается от (2.11) на посто­янный вектор. Например, для точки А имеем:

r а=fв(t) (2.12)

Таким образом, уравнение (2.11) определяет движение любой точки данного тела. В связи с этим это уравнение называется уравнением посту­пательного движения твердого тела в векторной форме.

Движение полюса В можно определить и уравнениями движения в координатной форме:

xB=f 1(t),

yb=f2(t) (2-13)

zB=f 3(t)

Уравнения движения любой другой точки данного тела отличаются от уравнений (2.13) постоянными членами. Например, для точки А будем иметь:

xB=f 1(t) +r x

yb=f2(t)+rx (2-14)

zB=f 3(t)+rz

где rx ry rz проекции на координатные оси постоянной вектора г . Таким образом, уравнения (2.13) определяют движение любой точки дан­ного тела и называются уравнениями поступательного движения твердого тела в координатной форме.

Аналогично, движение полюса В можно определить естественным способом с помощью уравнения: SB=fB(t). (2.15)

Это уравнение называется уравнением поступательного движения твердо­го тела в естественной форме. Уравнение движения других точек данного тела отличаются от него лишь постоянными членами, которые не оказы­вают влияние на скорость и ускорение его точек.

 Уравнение вращения твердого тела вокруг неподвижной оси

Если две точки А и В (рис. 2.7а) твердого тела закреплены неподвижно, то это тело сможет совершать только такое движение, при котором будут оставаться неподвижными все его точки, лежащие на прямой, проходящей через эти точки.

Эта прямая называется осью вращения. Оси вращения Z, как и всякой другой оси, приписывается определенное направление, считаемое положи­тельным.

Представим себе две полуплоскости Р и Q (рис. 2.7), ограниченные с одной стороны осью вращения Z, первая из которых неизменно связана с некоторой системой отсчета и, следовательно, условно считается непод­вижной, а вторая — с вращающимся твердым телом и, поэтому, вместе с ним вращается вокруг оси Z. На рис. 2.7 ось Z перпендикулярна к плоскости чертежа и, следовательно, на нем показаны лишь следы полуплоскостей Р и Q на этой плоскости.

Положение твердого тела однозначно оп­ределяется двугранным углом φ, образованным упомянутыми полуплоскостями, если считать его величиной алгебраической. Этот угол назы­вается угловой координатной твердого тела. Его принято считать положительным, если, при взгляде с положительного направления оси вращения, подвижная полуплоскость повернута относительно неподвижной против хода стрел­ки часов, и отрицательным в противном случае. Не следует смешивать угловую коорди­нату твердого тела с углом его поворота.

По­следний, как и путь, пройденный точкой, всегда положителен и может только увеличиваться, независимо от направления вращения тела.

Угловая координата, как правило, измеряется в радианах, т.е. являет­ся величиной безразмерной, и обозначается буквой φ. Иногда ее измеряют в полных оборотах тела и тогда обозначают буквой N. Поскольку один оборот содержит 2л радиан, то для перехода от одной единицы измерения угловой координаты к другой существует зависимость: φ = 2πN. (2.16)

При вращении твердого тела вокруг неподвижной оси его угловая координата, в общем случае, непрерывно изменяется с течением времени, т. е. является однозначной и, как показано ниже, дважды дифференцируе­мой функцией времени t, т.е.

φ = f(t). (2.17)

Уравнение такого вида определяет вращательное движение твердого тела и называется уравнением его вращения вокруг неподвижной оси.

Угловая скорость и угловое ускорение твердого тела

Угловая скорость твердого тела, вращающегося вокруг неподвижной оси, характеризует быстроту его вращения вокруг этой оси. Пусть в мо­мент t угловая координата тела равна φ, а в момент tx = t + Δt она равна φ = φ + Δφ. Следовательно, в течение бесконечно малого промежутка времени At тело поворачивается на бесконечно малый угол Δφ. Величина ωср = Δφ / Δt называется средней угловой скоростью тела за промежуток вре­мени Δt. Предел средней угловой скорости при Δt —0 называется угловой скоростью твердого тела в момент t и обозначается ω, т.е. ω =dφ / dt,

Таким образом, угловая скорость твердого тела, вращающегося во­круг неподвижной оси, равна первой производной его угловой координаты по времени.

Поскольку производная - dφ / dt, положительна при возрастании угловой

координаты φ и отрицательна в противном случае, то угловая скорость ω является величиной алгебраической. Она положительна, если тело враща­ется в сторону положительных угловых координат, т.е. против хода стрел­ки часов при взгляде с положительного направления оси вращения, и от­рицательна, если тело вращается в противоположном направлении.

Если угловую координату измерять в радианах, а время - в секундах, то, учтя, что радиан есть величина безразмерная, получим для угловой скорости ω размерность с' .

Иногда угловую скорость равномерного вращения твердого тела из­меряют числом его оборотов в минуту. В этом случае ее обозначают п. Между угловой скоростью ω (с ) и числом п (об/мин) существует зависи­мость: ω = πn / 30

Число п оборотов тела в минуту часто называют частотой его вращения.

Быстрота изменения угловой скорости характеризуется величиной его углового ускорения.

Пусть в момент t угловая скорость тела равна ω, а в момент t =t + Δt она равна

ω = ω + Δω. Тогда в течение бесконечно малого промежутка времени Δt угловая скорость тела изменяется на бесконечно малую величину Δω. Величина εср = Δω / Δt называется средним угловым ус­корением тела за промежуток времени Δt,, а ее предел при Δt —0 — угловым ускорением в момент t и обозначается ε, ε= dω / d t = d 2φ / d 2t =φ

Эта зависимость подтверждает высказанное выше предположение о том, что функция  должна быть дважды дифференцируемой.

Таким образом, угловое ускорение твердого тела, вращающегося во­круг неподвижной оси, в момент t равно первой производной его угловой скорости по времени или второй производной по времени его угловой ко­ординаты.

Угловое ускорение, также как и угловая скорость, является величи­ной алгебраической. Оно положительно, если угловая скорость увеличива­ется с течением времени и отрицательно в противном случае. Иными сло­вами, тело совершает ускоренное вращение, если угловая скорость и угло­вое ускорение имеют одинаковые знаки, и замедленное - если их знаки различны. Измеряется угловое ускорение в с-2.

. Плоское движение твердого тела

После ознакомления с кинематикой поступательного и вращательно­го движений твердого тела можно перейти к изучению кинематики более сложного его движения. Таким движением является плоское движение твердого тела.

П лоским движением твердого тела называется такое его движение, при котором все его точки перемещаются в плоскостях, параллельных не­которой неподвижной плоскости, называемой основной плоскостью. Плоское движение совершает, например, колесо, катящееся по прямоли­нейному рельсу, или шатун АВ (рис. 2.8) кривошипно-ползунного механизма, со­стоящего из кривошипа ОА, вращающегося

вокруг неподвижной оси О, перпендикулярной к плоскости чертежа, соединенного ним шарнирно шатуна АВ и ползуна В,

помещенного в горизонтальные направляющие и соединенного шарнирно с шатуном. Вращение твердого тела вокруг неподвижной оси и плоское поступательное движение являются частными случаями плоского движе­ния.

Пусть некоторое твердое тело (рис. 2.9) совершает плоское движе­ние. Понятно, что в этом случае плоская фигура S, образованная в сечении тела основной плоскостью Н (или плоскостью, ей параллельной), за все время движения тела остается в этой плоскости. Прямая AtA2, проходящая через произвольную точку А и фигуры S, перпендикуляр­ная к плоскости Н и неизмен­но связанная с рассматривае­мым телом, за все время дви­жения тела остается перпен­дикулярной к этой плоскости, т.е. совершает поступатель­ное движение Рис. 2.9. Следовательно, все точки этой прямой соверша­ют одинаковые движения.

То же самое можно сказать про точки прямых, параллельных прямой А,А2, проходящих через все остальные точки фигу­ры S. Отсюда следует, что все сечения данного тела плоскостями, парал­лельными плоскости Н, совершают одинаковые движения, следовательно, движение фигуры S в ее плоскости определяет плоское движение рассмат­риваемого твердого тела. Поэтому в дальнейшем вместо плоского движе­ния твердого тела мы будем исследовать движение плоской фигуры в ее плоскости.