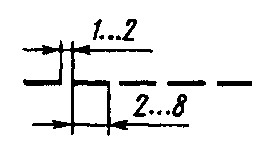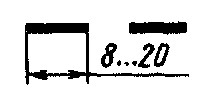1.1. Общие сведения о техническом черчении

Значение предмета. Назначение стандартов. Система стандартов.

Умение понимать язык чертежа, работать с чертежом и совершенствовать объект чертежа являются обязательными для каждого квалифицированного специалиста, связанного с эксплуатацией и ремонтом машин. Правильное понимание сведений и данных, приведённых в чертеже, - непременное условие изготовления качественных деталей, механизмов и устройств.

Каждый чертёж определяет конструкцию того или иного объекта (детали, механизма) и содержит все необходимые сведения для его разработки, изготовления, монтажа (сборки), контроля, эксплуатации и ремонта.  При выполнении чертежей используются стандарты, позволяющие грамотно их оформить и читать, которые объединены в комплекс под названием «Единая система конструкторской документации» (ЕСКД). Стандарты относятся к нормативной документации, устанавливающей единые правила выполнения и оформления конструкторских документов.

Стандарты ЕСКД подразделяются на следующие классификационные группы, каждой из которых присвоен шифр (0,…,9):

Таблица 1

Состав и классификация стандартов ЕСКД

0.	Общие положения
1.	Основные положения
2.	Классификация и обозначение изделий в конструкторских документах
3.	Общие правила выполнения чертежей
4.	Правила выполнения чертежей изделий машиностроения и приборостроения
5.	Правила обращения конструкторских документов (учет, хранение, дублирование, внесение изменений)
6.	Правила выполнения эксплуатационной и ремонтной документации
7.	Правила выполнения схем
8.	Правила выполнения документов строительных и судостроения
9.	Прочие стандарты

Обозначение стандартов ЕСКД

Все стандарты ЕСКД имеют следующую структуру обозначения:

ГОСТ 2. АВС – DЕ, где 2 – номер, присвоенный всему комплексу ЕСКД;

АВС – номер стандарта (А – шифр классификационной группы, ВС – порядковый номер в данной группе);

DЕ – последние две цифры года регистрации.

Например: ГОСТ 2.301-68 означает

2 – принадлежность к ЕСКД;

3 – классификационную группу - Общие правила выполнения чертежей;

01 – первый номер стандарта в группе;

68 – год издания 1968.

Общие правила оформления чертежей. Единая система конструкторской документации.

При оформлении чертежей применяют различные линии, назначение и начертание которых установлено ГОСТ 2.303-68 (Таблица 2): 

Таблица 2

Виды и начертание основных линий

Наименование	Начертание	Толщина линии по отношению к толщине основной линии	Основное назначение
1. Сплошная толстая основная		s	Линии видимого контура. Линии перехода видимые. Линии контура сечения (вынесенного и входящего в состав разреза).
2. Сплошная тонкая		От s/3  до s/2	Линии контура наложенного сечения. Линии размерные и выносные Линии штриховки. Линии-выноски. Следы плоскостей, линии построения характерных точек при специальных построениях.
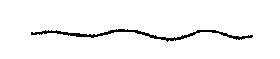
3. Сплошная волнистая			Линии обрыва. Линии разграничения вида и разреза.
4. Штриховая			Линии невидимого контура. Линии перехода невидимые.
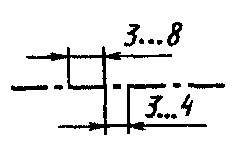
5. Штрихпунктирная тонкая		От s/3  до s/2	Линии осевые и центровые. Линии сечений, являющиеся осями симметрии для наложенных или вынесенных сечений.
6. Штрихпунктирная утолщённая		От s/3  до 2/3s	Линии, обозначающие поверхности, подлежащие термообработке или покрытию. Линии для изображения элементов, расположенных перед секущей плоскостью («наложенная проекция»).
7. Разомкнутая		От s до 11/2s	Линии сечений.
8. Сплошная тонкая с изломами		От s/3  до s/2	Длинные линии обрыва.
9. Штрихпунктирная с двумя точками тонкая		От s/3 до s/2	Линии сгиба на развертках. Линии для изображения частей изделий в крайних или промежуточных положениях. Линии для изображения развертки, совмещенной с видом.

Толщина линий одного типа должна быть одинаковой для всех изображений одного чертежа, вычерчиваемых в одном масштабе.

Форматы

Чертежи выполняются на листах бумаги определённых форматов, размеры которых установлены ГОСТ 2.301-68. Основные форматы представлены в таблице 3:

Таблица 3

Основные форматы (обозначения и размеры)

Обозначение	А4	А3	А2	А1	А0
Размеры сторон, мм	210×297	297×420	420×594	594×841	841×1189

Формат А0 принят за исходный, остальные получают делением предыдущего формата на две равные части параллельно внешней стороне.

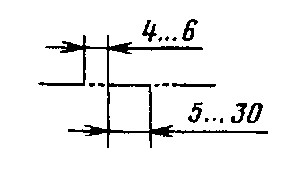
Формат листа определяется размерами внешней рамки, выполненной тонкой линией (Рисунок 1):

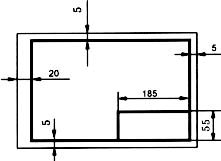
Рис. 1. Размеры внешней рамки.

Поле чертежа ограничивается сплошной толстой основной линией – рамкой. Линии рамки с трёх сторон (сверху, снизу и справа) отстоят от краёв формата на 5 мм, а слева – на 20 мм (Рисунок 1). Полоса слева используется для подшивки чертежа.

Оформление листа формата А1 представлено на рисунке 2. Основная надпись может располагаться вдоль короткой или вдоль длинной стороны формата. 

Основную надпись располагают в правом нижнем углу вплотную к рамке поля чертежа. Для всех чертежей ГОСТ 2.104-68* устанавливает единую форму, размеры и порядок оформления основной надписи. На листах А4 основную надпись располагают только вдоль короткой стороны. Форма и размеры основной надписи приведены на рисунке 3.

Основная надпись содержит графы, выполняемые чертёжным шрифтом:

• наименование изделия,
• обозначение номера чертежа,
• обозначение материала детали,
• масштаб изображения на чертеже,
• фамилии лиц, выполнивших и подписавших чертёж,
• дата подписания и т.д.

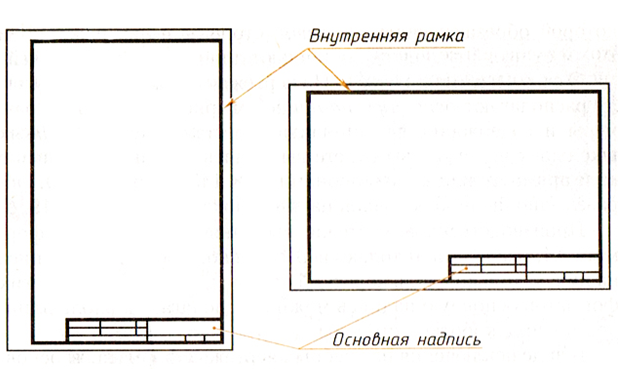
Рис. 2. Оформление листа формата А4.

а)

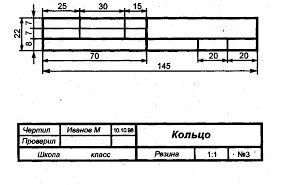
б)

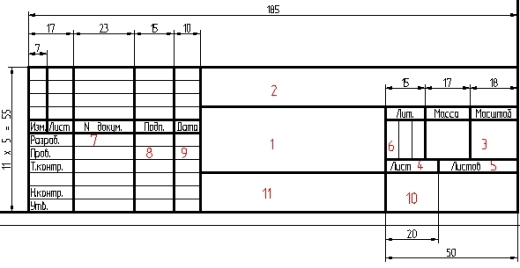
Рис. 3. Форма и размеры основной надписи.

а). Образец основной надписи для первого листа документов;

б). Образец формы основной надписи для второго и последующих листов.

Чертёжные шрифты

Шрифт – графическая форма изображения букв, цифр и условных знаков, используемая для выполнения технического документа. Выполнение их должно соответствовать  ГОСТ 2.304 – 81.

Размер (номер) шрифта обозначается буквой h и определяется высотой прописных букв в миллиметрах. Размер чертёжного шрифта, т.е. высота букв определена стандартом.

Стандарт устанавливает два типа шрифтов: А и В. В машиностроительном черчении наиболее распространён чертёжный шрифт типа В с наклоном под углом 75о. Толщина линий букв и цифр шрифта Б равна 1/10 h.

Начертание букв русского алфавита прописных и строчных шрифтом типа Б с наклоном, а также  арабских цифр, используемых при указании размеров и условных знаков, и  также образец надписи приведено на рисунке 4.

Рис. 4. Шрифт чертежный типа Б с наклоном около 75о (ГОСТ 2.304-81*).

Параметры шрифта типа Б с наклоном для букв русского алфавита и арабских цифр в относительных размерах приведены в таблице 4:

 Таблица 4

Шрифт типа Б (d = h/10)

Параметры шрифта	Обозначение	Относительный размер		Размеры, мм
Размер шрифта
высота прописных букв	h	(10/10) h	10d	1,8	2,5	3,5	5,0	7,0	10,0	14,0	20,0
высота строчных букв	с	(7/10) h	7d	1,3	1,8	2,5	3,5	5,0	7,0	10,0	14,0
Расстояние между буквами	а	(2/10)h	2d	0,35	0,5	0,7	1,0	1,4	2,0	2,8	4,0
Минимальный шаг строк (высота вспомогательной сетки)	b	(17/10)h	17d	3,1	4,3	6,0	8,5	12,0	17,0	24,0	34,0
Минимальное расстояние между словами	е	(6/10)h	6d	1,1	1,5	2,1	3,0	4,2	6,0	8,4	12,0
Толщина линий шрифта	d	(1/10)h	d	0,18	0,25	0,35	0,5	0,7	1,0	1,4	2,0

Геометрические построения. Основы проекционного черчения.

Построение перпендикуляров и углов.  Способы деления угла, отрезка и окружности на равные части. Сущность проецирования на плоскости. Прямоугольные проекции. Прямоугольное проецирование. Комплексный  чертёж. Расположение видов. Аксонометрические проекции.

На практике часто приходится выполнять геометрические построения. Это необходимо не только при составлении чертежа, но и при выполнении разметки перед изготовлением детали, при подготовке инструмента для её контроля в процессе обработки и эксплуатации. Поэтому важно уметь выполнять точные геометрические построения.

Построение перпендикуляров и углов.

Построение прямых углов.

На практике проведение прямой, параллельной заданной, выполняется с помощью чертёжных инструментов: двух угольников или линейки и угольника.

Угол 90° рационально строить с помощью рейсшины и угольника (Рис. 5). Для этого достаточно, проведя прямую линию, восставить к ней перпендикуляр с помощью угольника (Рис. 5, а). Рационально перпендикуляр к отрезку наклонной строить, передвигая (Рис. 5, б) или поворачивая (Рис. 5, в) угольник.

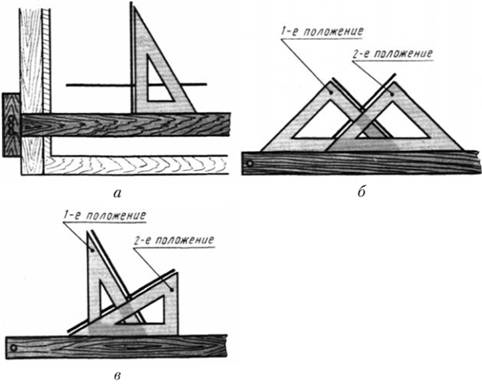
Рис. 5. Построение прямых углов с помощью угольников.

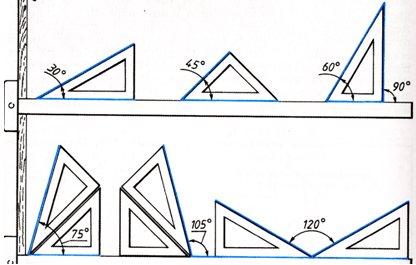
 Рис. 6. Построение острых и тупых углов.

Деление отрезка прямой.

Пусть отрезок АВ требуется разделить на пять равных частей. Для этого из любого конца отрезка (из точки А) проведём под острым углом к отрезку прямую линию, на которой откладываем пять равных отрезков произвольной величины. Точку 5 соединяем с точкой В (концом данного отрезка) заданной прямой. Из точек 1, 2, 3, 4 проведём ряд параллельных прямой 5А, которые, пересекая отрезок АВ, разделят его на пять равных частей (Рисунок 7).

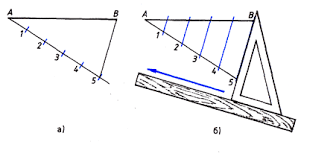
Рис. 7. Деление отрезка на пять равных частей.

Деление окружности на равные части.

Деление окружности на три и шесть равных частей выполняется в следующей последовательности (Рисунок 8а, 8г):

Деление окружности на три равные части производится следующим образом. Точка А (рис. 8а) принимается за центр, из которого проводится дуга, радиус которой равен радиусу окружности. Проведенная дуга пересечет окружность в точках С и Д. Дуги С-В, В-Д, Д-С являются третьей частью окружности. Соединив точки С, В и Д, получим правильный треугольник (Рисунок 8а).

Деление окружности на 4 равные части. Строим центровые линии, проводим окружность и определяем точки А, В, С, Д (концы диаметров), которые делят окружность на четыре равные части. Соединив отрезками прямых линий найденные точки, получаем правильный четырёхугольник (квадрат), вписанный в окружность (Рисунок 8б).

Деление окружности  на пять равных частей выполняется так: находим середину радиуса окружности ОВ (точка Е). Приняв точку В за центр, проведем дугу, радиус которой равен радиусу окружности, до пересечения ее с горизонтальным диаметром в точке О. Отрезок СЕ есть сторона пятиугольника. Отрезок ОЕ соответствует стороне правильного вписанного десятиугольника. Отложив величину, равную 1/5  окружности, разделим ее на пять  равных частей. Соединив последовательно засечки (вершины пятиугольника) отрезками прямых линий, получим правильный пятиугольник (Рисунок 8в).

Для деления окружности на шесть равных частей используют равенство сторон правильного шестиугольника радиусу описанной окружности, т. е. если дана окружность , то из концов одного из её диаметров (точек А и Е), как из центров, проводят дуги, равные радиусу окружности. Точки пересечения этих дуг с окружностью разделят её на шесть равных частей. Соединив данные точки отрезками в соответствующей последовательности, получаем правильный шестиугольник, каждая сторона которого равна радиусу окружности (Рисунок 8г).

Зная основы таких построений, можно разделить окружность на любое количество частей, используя правила вписанного и описанного многоугольника.

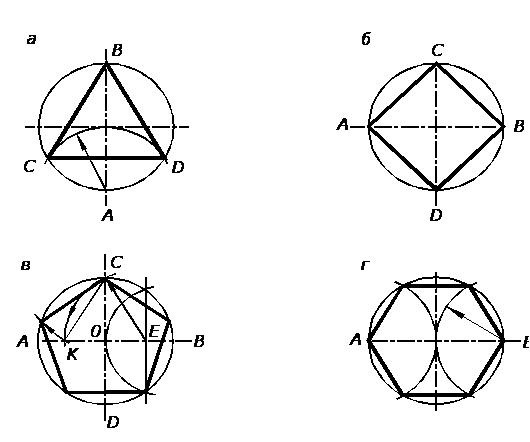
Рис. 8. Деление окружности на части.

Сущность проецирования на плоскости. Прямоугольные проекции. Прямоугольное проецирование.

Изображение пространственного объекта путём проведения линий на плоскости называют чертежом.

Геометрический объект (фигура) – это некоторое множество точек, объединённых между собой определёнными условиями. Для того чтобы отобразить весь геометрический объект, необходимо отобразить каждую из составляющих его точек. Способ, который используется для изображения геометрического объекта, называется метод проецирования. Результат этого действия называют проекцией.

Прямоугольное проецирование.

 

 

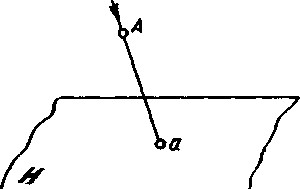
Рис. 9. Проецирование точки на плоскость.

Способ прямого проецирования является одним из приёмов отображения. Пусть в пространстве имеется точка А (Рисунок 9). Для получения проекции (отображения) этой точки на плоскость необходимо провести из неё проецирующий луч перпендикулярно к плоскости.  Точка а, в которой проецирующий луч пересекает плоскость проекций, является проекцией точки А на плоскость Н.

Принято использовать систему двух взаимно-перпендикулярных плоскостей проекций, предложенную Г. Монжем в 1799 г. (Рисунок 10). Одна из них, расположенная горизонтально, называется горизонтальной плоскостью проекций, а вторая, расположенная вертикально, - фронтальной плоскостью проекций. Линия пересечения плоскостей (ХО) называется осью проекций (Рисунок 10).

Для получения проекции точки А в системе двух взаимно-перпендикулярных плоскостей выполняют проецирование на  каждую плоскость. Пересечение проецирующего луча с горизонтальной плоскостью проекций определяет положение горизонтальной проекции точки а, пересечение проецирующего луча с вертикальной плоскостью проекций даст её фронтальную проекцию а/. 

Но пользоваться такими изображениями трудно, поэтому перешли к такому изображению, где обе проекции располагаются в одной плоскости.  Для этого горизонтальную и фронтальную плоскости совмещают, т. е. при неподвижной фронтальной плоскости проекций горизонтальную поворачивают вокруг оси Х так, чтобы передняя часть плоскости П1 опустилась (задняя часть плоскости П1 при этом поднимется). После совмещения плоскостей П1 и П2 получим чертёж, показанный на рис.10б. При этом фронтальная и горизонтальная проекции точки располагаются на одной прямой, перпендикулярной к оси x. Прямая а/а называется линией связи. На чертеже сам геометрический объект отсутствует, имеются только его отображения на плоскостях проекций.

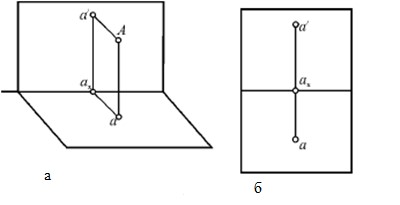
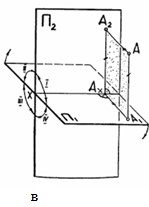
Рис. 10а, б, в. Система двух взаимно-перпендикулярных плоскостей проекций.

Рассмотрим проецирование точки А на три взаимно-перпендикулярные плоскости. К фронтальной и горизонтальной плоскостям добавим третью – профильную плоскость проекций (W), которую расположим перпендикулярно к плоскостям V и H. Используя метод ортогонального проецирования, изобразим точку на трёх плоскостях проекций. На профильной плоскости проекций получим изображение, которое будем называть профильной проекцией точки и обозначим её а// (Рисунок 11).

Плоскости проекций H и W разворачивают до совмещения с плоскостью V, как показано на рисунке 11.

Линии пересечения плоскостей являются осями проекций ox, oy, oz (Рисунок 11). Проекции а/ и а, а/ и а//, а и а// лежат на прямых, которые называют линиями проекционной связи (Рисунок 12). Такая зависимость в расположении проекции точки называется проекционной связью и при выполнении чертежей должна обязательно соблюдаться. Чертёж, состоящий из нескольких прямоугольных проекций, называется чертежом в системе прямоугольных проекций, или ортогональным чертежом.  

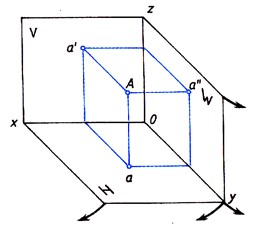
Рис. 11. Проецирование точки А на три плоскости проекций.

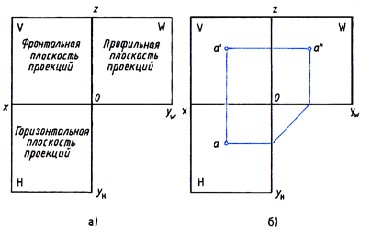
Рис. 12. Чертёж точки в системе прямоугольных проекций.

Расположение видов.

Чертёж представляет собой графическое изображение видимых и невидимых поверхностей предмета, которое получают прямоугольным (ортогональным) проецированием его на шесть граней куба при условии, что предмет расположен между наблюдателем и соответствующей гранью куба (Рисунок 9).  

При этом грани куба принимаются за основные плоскости проекций:

фронтальную – вид спереди,

горизонтальную – вид сверху,

профильную – вид слева,

и параллельные им плоскости (вид справа, вид снизу, вид сзади).

Для получения чертежа основных плоскостей с полученными на них изображениями совмещают в одну плоскость с фронтальной плоскостью проекций (Рисунок 13).

Видом называется изображение обращённой к наблюдателю видимой части поверхности предмета.

Различают основные, местные и дополнительные виды.

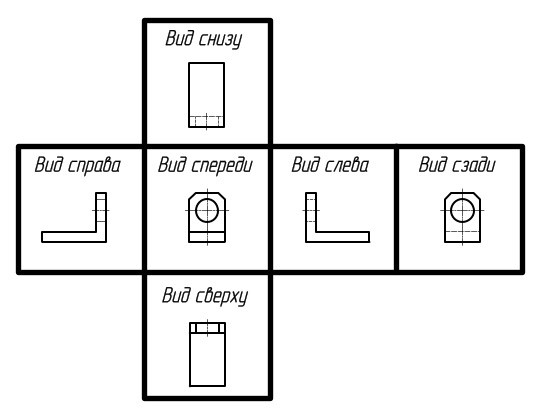
Рис. 13. Проецирование на плоскости.

Основные виды получают проецированием предмета на основные плоскости проекций (Рисунок 13). ГОСТ 2305-68* устанавливает следующие основные виды: вид спереди – главный вид, который даёт наиболее полное представление о размерах и форме предмета; вид сверху; вид слева; вид справа; вид снизу; вид сзади. Основные виды располагаются в проекционной связи относительно друг друга, поэтому не требуется наносить специальные надписи.

Рациональное расположение видов – это такое их расположение, при котором даётся полное представление о форме и всех особенностях изображаемой детали. 

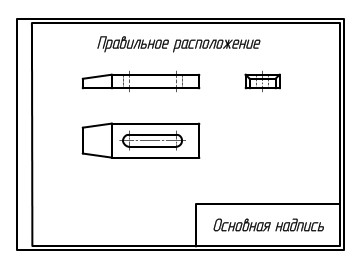
Рис. 14. Рациональное расположение видов.

Дополнительные виды применяют, если изображение предмета или какой-либо его части не может быть показано на основных видах без искажения форм и размеров. Их получают при помощи проецирования на плоскости, которые не являются параллельными относительно основным плоскостям проекций. Если дополнительный вид расположен в проекционной связи с исходным видом (Рисунок 15), то направление проецирования не указывают и надписи над ним не делают.

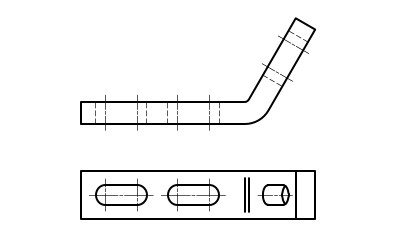
Рис. 15. Дополнительный вид.

Когда дополнительный вид невозможно расположить в  проекционной связи с исходным видом, его разрешается помещать на любом свободном месте чертежа с выполнением соответствующей надписи, например буквы А, при этом у исходного вида ставят стрелку с надписью А, указывающую направления проецирования (Рисунок 16).

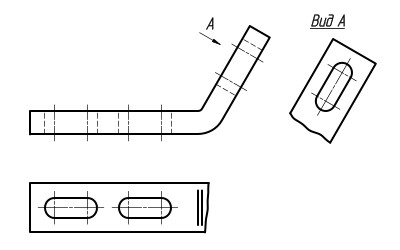
Рис. 16. Дополнительный вид со стрелкой и надписью.

Местным видом называется изображение отдельного ограниченного участка поверхности предмета, которое образуется его проецированием на одну из основных плоскостей проекций.

При его выполнении в проекционной связи с другим видом направление взгляда не указывается и надпись над ним не наносится (Рисунок 17). Допускается ограничение местного вида при помощи тонкой волнистой линии обрыва.

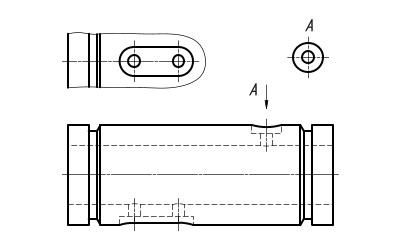
Рис. 17. Местный вид.

Изображение стрелок и соотношение их размеров приведено на рисунке 18.

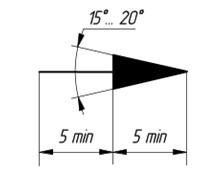
Рис.18. Изображение стрелок и их размеры.