1.1. Основы электротехники

Основы электротехники

Электротехника - это область науки и техники, изучающая электрические и магнитные явления и их использование в практических целях.
Каждая наука имеет свою терминологию. Запомним термины, понятия электротехники.
Электрическая цепь - это совокупность устройств, предназначенных для производства, передачи, преобразования и использования электрического тока.
Все электротехнические устройства по назначению, принципу действия и конструктивному оформлению можно разделить на три большие группы.

Источники энергии, т.е. устройства, вырабатывающие электрический ток (генераторы, термоэлементы, фотоэлементы, химические элементы).
Приемники, или нагрузка, т.е. устройства, потребляющие электрический ток (электродвигатели, электролампы, электромеханизмы и т.д.).
Проводники, а также различная коммутационная аппаратура (выключатели, реле, контакторы и т.д.).

Направленное движение электрических зарядов называют электрическим током. Электрический ток может возникать в замкнутой электрической цепи. Электрический ток, направление и величина которого неизменны, называют постоянным током и обозначают прописной буквой I.

Электрический ток, величина и направление которого не остаются постоянными, называется переменным током. Значение переменного тока в рассматриваемый момент времени называют мгновенным и обозначают строчной буквой i.

Для работы электрической цепи необходимо наличие источников энергии. В любом источнике за счет сторонних сил неэлектрического происхождения создается электродвижущая сила. На зажимах источника возникает разность потенциалов или напряжение, под воздействием которого во внешней, присоединенной к источнику части цепи, возникает электрический ток.

Различают активные и пассивные цепи, участки и элементы цепей. Активными называют электрические цепи, содержащие источники энергии, пассивными - электрические цепи, не содержащие источников энергии.

Электрическую цепь называют линейной, если ни один параметр цепи не зависит от величины или направления тока, или напряжения.
Электрическая цепь является нелинейной, если она содержит хотя бы один нелинейный элемент. Параметры нелинейных элементов зависят от величины или направления тока, или напряжения.

Электрическая схема - это графическое изображение электрической цепи, включающее в себя условные обозначения устройств и показывающее соединение этих устройств. На рис. 1.1 изображена электрическая схема цепи, состоящей из источника энергии, электроламп 1 и 2, электродвигателя 3.

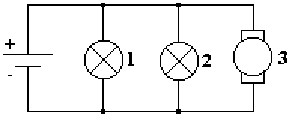
Рис. 1.1

 Для облегчения анализа электрическую цепь заменяют схемой замещения.
Схема замещения - это графическое изображение электрической цепи с помощью идеальных элементов, параметрами которых являются параметры замещаемых элементов.

На рисунке 1.2 показана схема замещения.

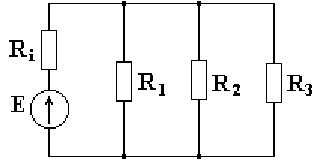
Рис. 1.2  Схема замещения

 Пассивные элементы схемы замещения

Простейшими пассивными элементами схемы замещения являются сопротивление, индуктивность и емкость.
В реальной цепи электрическим сопротивлением обладают не только реостат или резистор, но и проводники, катушки, конденсаторы и т.д. Общим свойством всех устройств, обладающих сопротивлением, является необратимое преобразование электрической энергии в тепловую. Тепловая энергия, выделяемая в сопротивлении, полезно используется или рассеивается в пространстве. В схеме замещения во всех случаях, когда надо учесть необратимое преобразование энергии, включается сопротивление.

Сопротивление проводника определяется по формуле

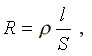      (1.1)

где l - длина проводника;
S - сечение;

r - удельное сопротивление.

Величина, обратная сопротивлению, называется проводимостью.

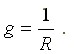
Сопротивление измеряется в омах (Ом), а проводимость - в сименсах (См).

Сопротивление пассивного участка цепи в общем случае определяется по формуле

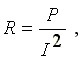
      где P - потребляемая мощность;
I - ток.
Сопротивление в схеме замещения изображается следующим образом:

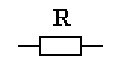
Индуктивностью называется идеальный элемент схемы замещения, характеризующий способность цепи накапливать магнитное поле. Полагают, что индуктивностью обладают только индуктивные катушки. Индуктивностью других элементов электрической цепи пренебрегают.

Индуктивность катушки, измеряемая в генри [Гн], определяется по формуле

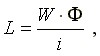
где W - число витков катушки;
Ф - магнитный поток катушки, возбуждаемый током i.

На рисунке показано изображение индуктивности в схеме замещения.

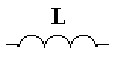
Емкостью называется идеальный элемент схемы замещения, характеризующий способность участка электрической цепи накапливать электрическое поле. Полагают, что емкостью обладают только конденсаторы. Емкостью остальных элементов цепи пренебрегают.

Емкость конденсатора, измеряемая в фарадах (Ф), определяется по формуле:

 

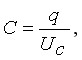
где q - заряд на обкладках конденсатора;
Uс - напряжение на конденсаторе.

На рисунке показано изображение емкости в схеме замещения

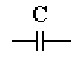
Активные элементы схемы замещения

Любой источник энергии можно представить в виде источника ЭДС или источника тока. Источник ЭДС - это источник, характеризующийся электродвижущей силой и внутренним сопротивлением.Идеальным называется источник ЭДС, внутреннее сопротивление которого равно нулю.

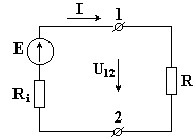
На рис. 1.3 изображен источник ЭДС, к зажимам которого подключено сопротивление R.
Ri - внутреннее сопротивление источника ЭДС.
Стрелка ЭДС направлена от точки низшего потенциала к точке высшего потенциала, стрелка напряжения на зажимах источника U12 направлена в противоположную сторону от точки с большим потенциалом к точке с меньшим потенциалом.
Рис.  1.3

Ток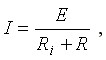     

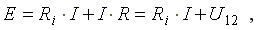   (1.2)

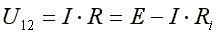     (1.3)

У идеального источника ЭДС внутреннее сопротивление Ri = 0, U12 = E.
Из формулы (1.3) видно, что напряжение на зажимах реального источника ЭДС уменьшается с увеличением тока. У идеального источника напряжение на зажимах не зависит от тока и равно электродвижущей силе.
Возможен другой путь идеализации источника: представление его в виде источника тока.
Источником тока называется источник энергии, характеризующийся величиной тока и внутренней проводимостью.

Идеальным называется источник тока, внутренняя проводимость которого равна нулю.

Поделим левую и правую части уравнения (1.2) на Ri и получим

,

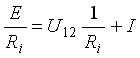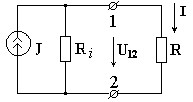
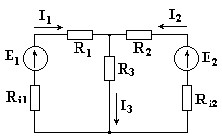      где 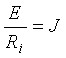   - ток источника тока;

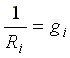               - внутренняя проводимость.

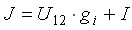
У идеального источника тока gi = 0 и J = I.

Ток идеального источника не зависит от сопротивления внешней части цепи. Он остается постоянным независимо от сопротивления нагрузки. Условное изображение источника тока показано на рис. 1.4.

Любой реальный источник ЭДС можно преобразовать в источник тока и наоборот. Источник энергии, внутреннее сопротивление которого мало по сравнению с сопротивлением нагрузки, приближается по своим свойствам к идеальному источнику ЭДС.

Если внутреннее сопротивление источника велико по сравнению с сопротивлением внешней цепи, он приближается по своим свойствам к идеальному источнику тока.

Основные определения, относящиеся к схемам

Различают разветвленные и неразветвленные схемы.
На рис. 1.5 изображена неразветвленная схема.
На рис. 1.6 показана разветвленная схема, содержащая два источника ЭДС и 5 сопротивлений.
Сопротивления соединительных проводов принимают равными нулю.

Разветвленная схема - это сложная комбинация соединений пассивных и активных элементов.
Сопротивления соединительных проводов принимают равными нулю.

Участок электрической цепи, по которому проходит один и тот же ток, называется ветвью. Место соединения двух и более ветвей электрической цепи называется узлом. Узел, в котором сходятся две ветви, называется устранимым. Узел является неустранимым, если в нем соединены три и большее число ветвей. Узел в схеме обозначается точкой.
Последовательным называют такое соединение участков цепи, при котором через все участки проходит одинаковый ток. При параллельном соединении все участки цепи присоединяются к одной паре узлов, находятся под одним и тем же напряжением.
Любой замкнутый путь, включающий в себя несколько ветвей, называется контуром.

Режимы работы электрических цепей

В зависимости от нагрузки различают следующие режимы работы: номинальный, режим холостого хода, короткого замыкания, согласованный режим.
При номинальном режиме электротехнические устройства работают в условиях, указанных в паспортных данных завода-изготовителя. В нормальных условиях величины тока, напряжения, мощности не превышают указанных значений.
Режим холостого хода возникает при обрыве цепи или отключении сопротивления нагрузки.
Режим короткого замыкания получается при сопротивлении нагрузки, равном нулю. Ток короткого замыкания в несколько раз превышает номинальный ток. Режим короткого замыкания является аварийным.

Согласованный режим - это режим передачи от источника к сопротивлению нагрузки наибольшей мощности. Согласованный режим наступает тогда, когда сопротивление нагрузки становится равным внутреннему сопротивлению источника. При этом в нагрузке выделяется максимальная мощность.

Основные законы электрических цепей

На рис. 1.6 изображен участок цепи с сопротивлением R. Ток, протекающий через сопротивление R, пропорционален падению напряжения на сопротивлении и обратно пропорционален величине этого сопротивления.

                                      
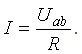
Падением напряжения на сопротивлении называется произведение тока, протекающего через сопротивление, на величину этого
Рис. 1.6 сопротивления.

Основными законами электрических цепей, наряду с законом Ома, являются законы баланса токов в разветвлениях (первый закон Кирхгофа) и баланса напряжений на замкнутых участках цепи (второй закон Кирхгофа). В соответствии с первым законом Кирхгофа, алгебраическая сумма токов в любом узле цепи равна нулю:

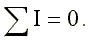
Возьмем схему на рис. 1.7 и запишем для нее уравнение по первому закону Кирхгофа.

Токам, направленным к узлу, присвоим знак "плюс", а токам, направленным от узла - знак "минус". Получим следующее уравнение:
 Рис. 1.7

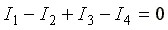или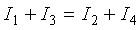

Согласно второму закону Кирхгофа, алгебраическая сумма ЭДС вдоль любого замкнутого контура равна алгебраической сумме падений напряжений в этом контуре

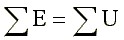
Возьмем схему на рис. 1.8 и запишем для внешнего контура этой схемы уравнение по второму закону Кирхгофа.

    

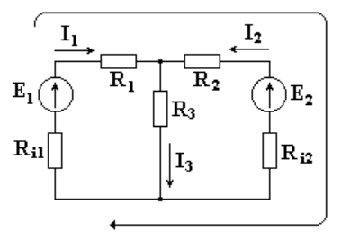
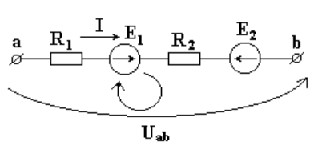
Рис. 1.9 Направления пути отхода

Для этого выберем произвольно направление обхода контура, например, по часовой стрелке. ЭДС и падения напряжений записываются в левую и правую части уравнения со знаком "плюс", если направления их совпадают с направлением обхода контура, и со знаком "минус", если не совпадают.

При определении тока в ветви, содержащей источник ЭДС, используют закон Ома для активной ветви.

Возьмем ветвь, содержащую сопротивления и источники ЭДС. Ветвь включена к узлам a-b, известно направление тока в ветви 

Возьмем замкнутый контур, состоящий из активной ветви и стрелки напряжения Uab, и запишем для него уравнение по второму закону Кирхгофа. Выберем направление обхода контура по часовой стрелке.

Получим

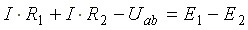
Из этого уравнения выведем формулу для тока

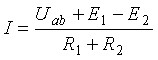
В общем виде:

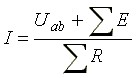
где R - сумма сопротивлений ветви;
E - алгебраическая сумма ЭДС.

ЭДС в формуле записывается со знаком "плюс", если направление ее совпадает с направлением тока и со знаком "минус", если не совпадает.

Электрические цепи переменного однофазного тока

Переменный ток широко применяется в различных областях электротехники. Электрическая энергия почти во всех случаях производится, распределяется и потребляется в виде энергии переменного тока.

Широкое применение переменного тока в различных областях техники объясняется легкостью его получения и преобразования, а также простотой устройства генераторов и двигателей переменного тока, надежностью их работы и удобством эксплуатации.

Генерирование переменного электрического тока практически легче осуществляется в машинах с вращающимися проводниками.

Переменный ток, меняет свое значение и направление определенное число раз в секунду. При переменном токе электроны движутся вдоль провода сначала в одном направлении, затем на мгновение останавливаются, далее движутся в обратную сторону, опять останавливаются и снова повторяют движение вперед и назад. То есть электроны совершают в проводе колебания. Вследствие своей малой скорости движения (Vэл = 10-4 м/с = 0,1 мм/с ) электроны при таких колебаниях успевают сделать лишь небольшие перемещения вдоль провода.

Наиболее часто встречается, так называемый синусоидальный переменный ток. Изменение электрических величин (силы тока, напряжения, э.д.с.) со временем показывает плавная кривая линия, называемая синусоидой.

Электрические цепи, в которых значения и направления э.д.с., напряжения и тока периодически изменяются со временем по синусоидальному закону, называются цепями синусоидального тока. Иногда их называют просто цепями переменного тока.

Для переменного тока была выбрана синусоидальная форма, так как она обеспечивает более экономичные производство, передачу, распределение и использование электрической энергии.

Кроме того именно синусоидальная форма электрических величин остается неизменной во всех участках сколь угодно сложной электрической цепи, то есть индуктивные и емкостные элементы входящие в состав электрических цепей не изменяют синусоидальной формы.

В большинстве стран выбрана частота переменного тока 50 Гц (США и Канада - 60 Гц). Эта частота является наиболее оптимальной, поскольку переменные токи низкой частоты 25 - 40 Гц вызывают заметное для глаза мигание электрических ламп накаливания, а повышение частоты приводит к росту э.д.с. самоиндукции и дополнительным потерям при передаче электроэнергии.

Рассмотрим процесс возникновения синусоидальной э.д.с. Простейшим генератором синусоидальной э.д.с. может служить прямоугольная рамка, равномерно вращающаяся в однородном магнитном поле с угловой скоростью w. Пронизывающий катушку (рамку) магнитный поток во время вращения рамки abcd индуцирует в ней на основании закона электромагнитной индукции э.д.с. е.

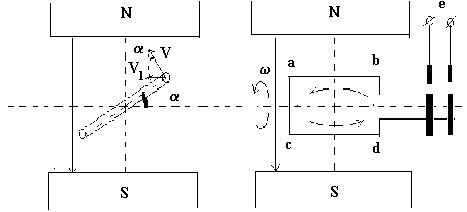
Нагрузку подключают к генератору с помощью щеток, прижимающихся к двум контактным кольцам, которые соединены с катушкой (рамкой).

Значение наведенной в рамке э.д.с. в каждый момент времени пропорционально магнитной индукции В, размеру активной части рамки l = ab + cd , скорости пересечения магнитных линий VH :

e = BlVH.

Причем скорость VH зависит от ориентации рамки :

VH = V sin a,

где V - линейная скорость движения рамки, a - угол описывающий положение рамки (ориентацию относительно вектора магнитной индукции).

В случае равномерного вращения рамки угол поворота зависит от времени следующим образом :

a = wt.

Следовательно, э.д.с. индуцируемая в равномерно вращающейся рамке определяется :

e = BlVsinwt.

Сомножители, стоящие перед sin wt представляют собой максимальное значение наведенной э.д.с. :

em = BlV.

Тогда

e = emsin wt.

Если в начальный момент времени рамка распологалась не по нормали к силовым линиям, а под углом je то a = wt + je и

e = emsin (wt+ je ).

Электрические цепи переменного тока по сравнению с цепями постоянного тока имеют ряд особенностей. Эти особенности определяются во-первых, тем, что в состав цепей переменного тока входят новые элементы: трансформаторы, конденсаторы, катушки индуктивности, во-вторых тем, что переменные токи и напряжения в этих элементах порождают переменные электрические и магнитные поля, которые в свою очередь приводят к возникновению явления самоиндукции, взаимной индукции и токов смещения.

Все это оказывает существенное влияние на протекающие электрической цепи процессы. Анализ процессов в цепях усложняется.

В резисторах в цепях постоянного тока электрическая энергия преобразуется в тепловую. В цепях переменного тока помимо преобразования электрической энергии в тепловую происходит накапливание энергии в магнитном и электрическом полях, то есть кроме параметра сопротивления R, цепь характеризуется еще и параметрами индуктивности и емкости L, C.

Для цепи переменного синусоидального тока большое значение имеет частота f. От частоты зависит влияние емкостей и индуктивностей на процессы в цепи.

Особенности цепей синусоидального тока обуславливают ряд новых, специфических для этих цепей явлений : сдвиг фаз, явление резонанса, появление реактивных мощностей.

При расчете режимов цепи синусоидального тока максимально используются понятия, формулы и методы расчета цепей постоянного тока.

В цепях переменного тока направление э.д.с., токов и напряжений изменяются два раза за период. Однако при расчете цепи синусоидального тока необходимо составлять уравнения по законам Кирхгофа, а они требуют задания определенных направлений э.д.с., токов и напряжений. Поєтому положительные направления токов, как и для цепи постоянного тока, выбирают произвольно.

Законы Кирхгофа, расмотренные ранее для цепей постоянного тока, справедливы и для мгновенных значений синусоидальных токов, напряжений и э.д.с.

Первый закон Кирхгофа :

Алгебраическая сумма мгновенных значений токов в узле равна нулю :

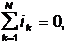
где N - число ветвей, соединенных в узле.

Второй закон Кирхгофа :

Алгебраическая сумма напряжений на резистивных, индуктивных и емкостных элементах контура в данный момент времени равна алгебраической сумме э.д.с. в том же контуре в тот же момент времени.

При составлении уравнений контур обходят в одном произвольно выбранном направлении, алгебраически суммируя напряжения и э.д.с. Если положительное направление напряжения и э.д.с. совпадает с направлением обхода, то это напряжение или э.д.с. записываются со знаком “ + ” плюс, если не совпадает, то со знаком “ - ”.

Закон Ома для мгновенных значений напряжения и тока справедлив только для резистивных элементов ( I = U/R ).

Параметры переменного тока

Для количественной характеристики переменного тока служат служат следующие параметры.

Мгновенные значения тока, напряжений и э.д.с. - это их значения в любой момент времени:

i = imsin (wt+ ji ), u = umsin (wt+ ju ),

e = emsin (wt+ je ).

Амплитудные значения тока, напряжения и э.д.с. im ,um ,em - максимальные значения мгновенных значений.

Период Т - промежуток времени, в течение которого ток совершает полное колебание и принимает прежнее по величине мгновенное значение. Период измеряется в секундах.

Угловая частота w - характеризует скорость вращения катушки генератора в магнитном поле. Измеряется в рад/с. Связана с периодом следующей формулой :

w = 2p/Т.

Циклическая частота (частота) f - величина, обратная периоду и характеризующая число полных колебаний тока за 1с. Частота измеряется [Гц] = 1/с и определяется :

f = 1/Т.

Частота и угловая частота связаны между собой следующим образом :

w = 2pf.

Фаза. Аргументы периодических функций называют фазой. Фазы характеризуют значения соответствующих величин в заданный момент времени. Значение фазы в начальный момент времени называется начальной фазой. Начальная фаза определяет значение соответствующей величины в начальный момент времени.

Действующие значения I, U, E. Пользоваться амплитудными значениями тока и напряжения не всегда удобно. Например, очевидно, что переменный ток с амплитудой 10 А имеет меньшую мощность, чем постоянный ток 10 А. Значение постоянного тока все время равно 10 А, а переменный ток достигает 10 А только в моменты, соответствующие амплитудному значению. В другие моменты ток меньше 10 А и даже доходит до нуля.

За основу для измерения постоянного тока положено сопоставление его среднего теплового действия с тепловым действием постоянного тока. Определенное посредством такого сравнения значение силы тока называется действующим значением.

Действующим значением переменного тока называется такой постоянный ток, при котором выделяется в резистивном элементе с активным сопротивлением R за период то же количество энергии, что и при действии переменного тока.

Энергия, которая выделяется в резистивном элементе при переменном токе :

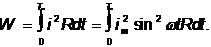
При постоянном токе выделяется энергия :

.

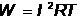Приравнивая правые части получим действующее значение тока :

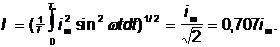
Таким образом, действующее значение тока меньше амплитудного в раз. Аналогично определяются действующие значения э.д.с. и напряжения.

Когда говорят о значении напряжения, э.д.с. и тока в цепях переменного тока, то имеют в виду их действующие значения. Шкалы измерительных приборов переменного тока проградуированы в действующих значениях. Например, если прибор показывает 10 А, то это значит, что амплитуда тока :

im = I = 1,41 × 10 = 14,1 A,

Напряжение в сети 220 В означает, что действующее напряжение в осветительной сети составляет 220 В. Амплитудное значение напряжения в осветительной сети равно 311 В. Амплитудное значение напряжения нужно принимать во внимание, например при выборе изоляции.

Метод векторных диаграмм

Электрическое состояние цепей переменного тока, так же как и цепей постоянного тока, описывается уравнениями Кирхгофа. Однако при анализе цепей переменного синусоидального тока математический аппарат становится очень громоздким, так как все уравнения содержат электрические величины, изменяющиеся по гармоническому закону.

Для упрощения анализа и расчета цепей переменного тока в электротехнике используют метод векторных диаграмм.

В электротехнике векторами изображаются изменяющиеся гармонически э.д.с., напряжения и токи, но в отличие от векторов, которыми изображались силы и скорости в механике, эти вектора вращаются с постоянной угловой скоростью и не означают направления действия.

Допустим, что радиус-вектор ОА, представляющий собой в определенном масштабе амплитудное значение э.д.с. em вращается с постоянной угловой частотой w = 2pf против часовой стрелки. Проекция ОА на OY будет равна

Oa = OA sin a.

Выразив ОА через амплитудное значение э.д.с. em и угол a через wt , получим выражение мгновенного значения э.д.с. изменяющейся синусоидально :

e = em sin wt.

График мгновенных значений э.д.с. изображен в правой части рисунка.

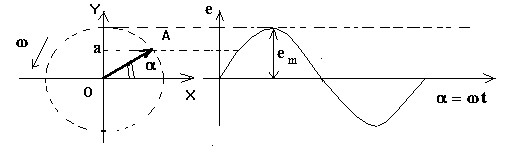
За начало отчета выбран момент времени, когда радиус-вектор совпадает с горизонтальной осью ( ось Х ). Если в начальный момент времени t = 0, ОА совпадает с линией, расположенной под углом j к оси Х, то проекция ОА, а следовательно, и э.д.с. будут соответственно равны :

Oa = OA sin (wt + j), e = em sin (wt + jе).

Аналогично можно представить в виде векторов, вращающихся против часовой стрелки с постоянной угловой частотой w, напряжение и ток.

Совокупность нескольких вращающихся векторов, в начальный момент времени, соответствующих уравнениям электрической цепи, называется векторной диаграммой.

Обычно векторные диаграммы строят не для амплитудных значений, а для действующих значений. При построении векторных диаграмм обычно один из векторов распологают на плоскости произвольно, остальные же вектора - под соответствующими углами к исходному. При этом в подавляющем большинстве случаев можно обойтись без нанесения осей координат.

Векторные диаграммы позволяют, не прибегая к вычислениям, исследовать характер изменений той или иной величины, определяющей режим работы электрической цепи.

Анализ электрических цепей переменного синусоидального тока

В общем случае электрическая цепь переменного тока может содержать резистивные, индуктивные и емкостные элементы, параметрами которых являются сопротивление, индуктивность и емкость.

Анализ и расчет таких цепей значительно сложней, чем цепей постоянного тока. Прежде чем разбирать общий случай цепи содержащей все выше перечисленные элементы рассмотрим частные случаи.

.Электрическая цепь с активным сопротивлением.

Рассмотрим электрическую цепь, содержащую только резистивный элемент с активным сопротивлением. Под активным сопротивлением понимают сопротивление проводников переменному току. Активные сопротивления непрерывно потребляют энергию.

Сопротивление резистора в цепи переменного тока может отличаться от сопротивления того же резистора в цепи постоянного тока. Это различие обусловлено поверхностным эффектом, при котором ток вытесняется к поверхности проводника, и зависит от частоты. С увеличением частоты сопротивление растет. Однако при относительно небольших частотах, например 50 Гц, его увеличением можно пренебречь.

Рассмотрим цепь состоящую из источника э.д.с.

e = em sin wt.

и резистора сопротивлением R :

Если r << R, то ток в цепи зависит главным образом от э.д.с. и сопротивления нагрузки - источник в этом случае называют источником э.д.с. или напряжения, так как на его выводах

e= u.

Поэтому в цепи переменного тока действует напряжение :

u = um sin wt.

Мгновенное значение силы тока в цепи с активным сопротивлением определяется законом Ома:

i = u / R = um sin wt /R = im sin wt.

Отсюда следует закон Ома для амплитудных значений :

im = um / R,

а разделив левую и правую части равенства на, получим закон Ома для действующих значений :

I = U / R.

Сопоставляя выражения для мгновенных и действующих значений тока и напряжения, можно прийти к выводу, что токи и напряжения в цепи с активным сопротивлением совпадают по фазе.

Векторная диаграмма для цепи с активным сопротивлением имеет вид :

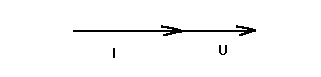
Мгновенная мощность цепи равна произведению мгновенных значений тока и напряжения. Мощность определяет скорость расхода энергии, и следовательно, для цепей переменного тока является величиной переменной.

Мгновенная мощность, оставаясь все время положительной колеблется около уровня UI.

В цепи с активным сопротивлением энергия все время поступает от источника к приемнику и необратимо преобразуется в нем в теплоту и рассеивается в окружающей среде.

Для определения расхода энергии за длительное время целесообразно пользоваться средним значением мощности. Для вывода выражения средней мощности найдем сначала расход энергии в цепи за полупериод :

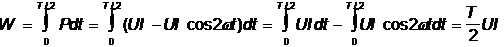
Разделив полученное выражние на Т / 2, получим среднюю скорость расхода энергии:

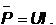
Электрическая энергия, которая преобразуется на активном сопротивлении в тепловую называется активной мощностью.

Активная мощность измеряется ваттметром.

Электрическая цепь с индуктивным элементом.

Огромное влияние на процессы протекающие в цепях имеет явление электромагнитной индукции.

Явление электромагнитной индукции заключается в том, что изменение магнитного поля вокруг проводника, связанное с пересечением проводника магнитными силовыми линиями, вызывает появление э.д.с. в этом проводнике.

При этом безразлично, будет ли изменяться магнитное поле относительно проводника или проводник будет перемещаться в магнитном поле.

При изменении тока в проводнике изменяется магнитный поток, создаваемый этим током. Изменение магнитного потока индуцирует в проводнике э.д.с., действие которой по правилу Ленца направлено на поддержание предшествующего состояния поля (Правило Ленца: Индуцируемая э.д.с. стремится противодействовать причине, ее вызывающей). Такое явление называется самоиндукцией. Явление самоиндукции в проводниках характеризуется индуктивностью L. Индуктивность это размерный коэффициент пропорциональности между скоростью изменения тока во времени и индуцируемой при этом э.д.с.

e = - L×(di / dt)

Знак минус в формуле отражает правило Ленца. Индуктивность измеряется в Генри.

Значение индуктивности L зависит от конструкции элементов цепи. Так для катушки с числом витков N, магнитопроводом длины l, площади S и магнитной проницаемостью m:

L = m0×m×N2×S / l

Индуктивностью обладают также одиночный прямой провод, двухпроводная линия, коаксиальный кабель.

Обмотки электрических машин, трансформаторов, реле, катушки индуктивности обладают значительной индуктивностью.

Переменный ток встречает в проводниках не только омическое сопротивление. Непрерывное противодействие э.д.с., препятствующее изменению переменного тока, создает в цепи дополнительное сопротивление. Это дополнительное сопротивление называют индуктивным сопротивлением. Таким образом, катушки и разные обмотки, поскольку в них есть индуктивность, оказывают большее сопротивление переменному току, чем постоянному.

Параметрами катушек индуктивности являются активное сопротивление и индуктивность.

Рассмотрим вначале катушку, активное сопротивление которой настолько мало, что им можно пренебречь. Применим к рассматриваемому замкнутому контуру второй закон Кирхгофа.

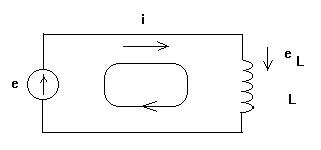
В случае цепей переменного тока второй закон Кирхгофа формулируется для мгновенных значений следующим образом:

Алгебраическая сумма напряжений на всех элементах контура в данный момент времени равна алгебраической сумме э.д.с. в том же контуре, в тот же момент времени.

При составлении уравнений контур обходят в одном произвольно выбранном направлении, алгебраически суммируя напряжения и э.д.с.

Если положительное направление напряжения и э.д.с. совпадает с направлением обхода контура, то это напряжение или э.д.с. записываются со знаком “ + “, если не совпадают, то со знаком " - ".

Под действием синусоидального напряжения в цепи с катушкой протекает синусоидальный ток :

i = im sin wt.

В результате вокруг этой катушки возникает переменное магнитное поле и в катушке наводится э.д.с. самоиндукции.

e + eL = 0.

При исследовании цепей с э.д.с. самоиндукции условились положительное направление э.д.с. самоиндукции брать совпадающим, с положительным направлением тока, который наводит эту э.д.с. Но э.д.с. источника равна его внешнему напряжению (у источника э.д.с. внутреннее сопротивление r » 0 и э.д.с. не зависит от тока нагрузки проходящего через источник e = u = const):

e = u,

а э.д.с. самоиндукции и ток связаны уравнением :

eL = - L di/dt.

Если ток со временем увеличивается, то di/dt > 0 и eL < 0, то есть ток самоиндукции направлен навстречу току, обусловленному внешним источником, и тормозит его возростание. Если ток со временем падает, то di/dt < 0 и eL > 0, то есть индукционный ток имеет тоже направление как и убывающий ток в контуре, и замедляет его убывание. Таким образом, контур, обладая индуктивностью, приобретает электрическую инертность, заключающуюся в том, что любое изменение тока тормозится тем сильнее, чем больше индуктивность.

Второй закон Кирхгофа для рассматриваемой электрической цепи :

u = -eL.

Напряжение источника целиком идет на уравновешивание eL.

u = L di/dt = im wL cos wt = um sin ( wt + p/2 ), где

um = im wL.

Сопоставляя мгновенные значения тока и напряжения приходим к выводу, что ток в цепи с индуктивным элементом отстает по фазе от напряжения на p/2.

Векторная диаграмма цепи с индуктивным элементом имеет вид :

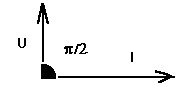
Выведем закон Ома для этой цепи. Из um = im wL следует, что im=um/wL. Введем обозначение:

ХL = wL.

Эта величина называется реактивным индуктивным сопротивлением, или просто индуктивным сопротивлением.

Закон Ома для мгновенных значений:

im=um / ХL

Закон Ома для действующих значений :

I = U / ХL.

С увеличением частоты тока индуктивное сопротивление увеличивается. Физически это объясняется тем, что возрастает скорость изменения тока, а следовательно, и э.д.с. самоиндукции.

Иногда необходимо увеличить сопротивление в цепи переменного тока, в этом случае в цепь включают катушку со стальным сердечником, называемую дросселем. Большая самоиндукция мешает увеличению тока и поддерживает его в моменты спада. Дроссели применяются: в электросварке, в различных выпрямителях, в радиотехнических устройствах. Для защиты электрических сетей от токов короткого замыкания устанавливают реакторы - большие катушки из толстого медного провода. Для обычного перменного тока они представляют очень небольшое сопротивление. При мгновенном увеличении тока короткого замыкания в реакторе индуктируется большая э.д.с. самоиндукции. Она противодействует этому увеличению и ограничивает ток короткого замыкания до безопасной величины, чем защищает ценное оборудование - генераторы, трансформаторы, электродвигатели - от разрушения.

Обычно катушки и обмотки имеют значительное индуктивное сопротивление. Когда нужно, чтобы катушка в цепи переменного тока не имела индуктивного сопротивления, а только активное, то провод на катушку накладывают так: весь провод складывают вдвое и тогда наматывают на катушку. Обмотка выполненная таким образом, называется бифилярной, или двухвитковой.

Осутствие индуктивности в таких катушках обьясняется тем, что магнитные поля, создающиеся противоположно направленными токами в двух половинах обмотки, взаимно компенсируются. Поэтому катушка в целом не создает магнитного потока и в ее витках не индуктируется э.д.с.

Среднее значение мощности:

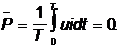
Физически это объясняется преобразованием энергии источника в энергию магнитного поля катушки и возвращением накопленной энергии источнику. В среденем катушка не потребляет энергии, и следовательно, активная мощность P = 0.

Для количественной характеристики интенсивности обмена энергией между источником и индуктивными элементами служит величина называемая реактивной мощностью:

Q = UI.

Измеряется реактивная мощность в единицах, которые называются вольт-ампер реактивный или сокращенно вар.

Реактивными называются сопротивления, которые в среднем не потребляют энергию.

Электрическая цепь с емкостным элементом.

Если в цепь постоянного тока подключить конденсатор, то тока в цепи не будет, так как она разрывается диэлектриком, находящимся между пластинами конденсатора.

При включении конденсатора в цепь переменного тока обнаружим, что ток проходит по цепи, несмотря на ее разрыв диэлектриком в конденсаторе.

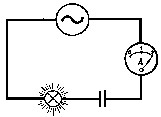
Чтобы понять, почему переменный ток проходит по цепи, рассмотрим работу установки; изображенную на рисунке:

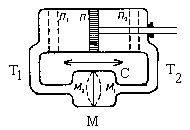
Поршень П двигается в цилиндре вправо и влево. В сосуде С имеется упругая перепонка М, которая делит цепь на две части. При перемещении поршня влево вода, опускаясь по трубе Т1, начнет давить на перепонку М, которая, выгнувшись, займет положение М1; в трубе Т2 вода в этот момент будет подниматься вверх.

Непрерывное перемещение поршня создает непрерывное движение жидкости в цепи. Перепонка периодически выгибается то вправо, то влево, создавая давление на воду.

Источник переменного тока выполняет работу, подобную поршню, а конденсатор в цепи переменного тока можно сравнить с упругой перепонкой. Напряжение электрической цепи похоже на давление поршня на воду, а перемещение воды имеет сходство с током в электрической цепи. Напряжение источника периодически меняет свой знак. Поэтому за первый полупериод одна обкладка конденсатора заряжается положительно, а другая - отрицательно.

В начале следующего полупериода меняется знак напряжения источника, и конденсатор перезаряжается.

При каждой перезарядке конденсатора по цепи то в одном, то в другом направлении будет проходить ток. Этот ток не проходит сквозь диэлектрик конденсатора, так же, как вода не проходит сквозь перепонку М. Когда ток перезарядки конденсатора проходит через лампу, то он накаляет ее нить.

Такой ток называют емкостным током. Таким образом, переменный ток по цепи с конденсатором проходит.

Проанализируем процессы в цепи емкостным элементом. Зададимся напряжением на зажимах источника

u = um sin wt,

тогда ток в цепи также будет изменяться по синусоидальному закону. Ток определяется по формуле :

i = dq/dt.

Электрический заряд на обкладках конденсатора связан с напряжением на конденсаторе и его емкостью формулой :

q = Cu.

Следовательно :

i = dq/dt = Cdu/dt = um wС cos wt = um wС sin ( wt + p/2 ).

Таким образом, ток в цепи с емкостью опережает по фазе напряжение на угол p/2.

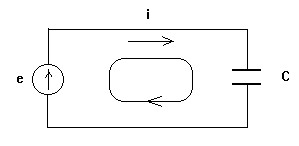
Векторная диаграмма напряжения и тока для цепи с емкостным элементом имеет вид :

Физически это объясняется тем, что напряжение на конденсаторе возникает за счет разделения зарядов на его обкладках в результате протекания тока. Следовательно, напряжение появляется только после возникновения тока.

Получим закон Ома для цепи с емкостным элементом. В формуле :

i = um wС sin ( wt + p/2 )

введем обозначение

Хc = 1 / wС,

где Хc - емкостное сопротивление.

Закон Ома для амплитудных и действующих значений имеет вид :

im = um / Хc, I = U / Xc.

Емкостное сопротивление уменьшается с ростом частоты. Это объясняется. тем что при большой частоте через поперечное сечение диэлектрика в единицу времени протекает больший заряд при том же напряжении, что эквивалентно уменьшению сопротивления в цепи.

Рассмотрим энергетические характеристики в цепи с емкостью. Пусть начальная фаза тока в цепи равна нулю, тогда

i = im sin wt .

Поскольку напряжение на емкости отстает от тока на угол p/2 , то

u = um sin ( wt - p/2 ) = - um сos wt.

Мгновенная мощность вычисляется по формуле :

p = ui = - um im sin wt сos wt = - UI sin 2wt.

Графики напряжения, тока и мгновенной мощности показаны ниже на рисунке. В цепи с емкостью, так же как в цепи с индуктивностью, происходит переход энергии от источника к нагрузке, и наоборот. В данном случае энергия источника преобразуется в энергию электрического поля конденсатора и наоборот. Средняя активная мощность в цепи с емкостью также равна нулю.

Для количественной характеристики интенсивности обмена энергией между источником и конденсатором служит реактивная мощность:

Q = UI.