1.1. Основы технической механики

Статика и ее основные понятия и определения.

В механике изучаются законы взаимодействия и движения твердых тел.

Механическим движением называется происходящее с течением времени изменение положения точек или тел в пространстве. Частным случаем движения является состояние покоя. Покой всегда имеет относительный характер, так как покоящееся тело рассматривается как неподвиж­ное по отношению к другому телу, которое, в свою очередь, может перемещаться в пространстве.

Абсолютно твердым телом называется тело, когда расстояние между любыми его точками не меняется при действии на него других тел. В статике полагают, что тела абсолютно твердые и их физико-механические свойства не учитывают.

В статике любое тело можно считать материальной точкой, размерами которого в условиях данной задачи можно пренебречь.

Материальной точкой называется точка, имеющая массу.

Свободным называется тело, когда никакие другие тела не препятствуют его перемещению в любом направлении. В противном случае тело называется несвободным.

Сила есть мера механического взаимодействия тел. Она характеризу­ется числовым значением, направлением и точкой приложения. Из этого следует, что сила — величина векторная. Числовое значение силы называется модулем вектора силы. Направление силы есть направление того движения, которое получила бы покоящаяся свободная материальная точка под действием этой силы.

Линия действия силы - это прямая линия, по которой направлен вектор силы.

Единицей измерения силы в системе СИ является Ньютон (Н) -это сила, сообщаемая телу массой 1 кг ускорение 1м/с в направлении действия силы. Допускаются внесистемные единицы: килограмм-сила (КС, КГ), тонна-сила (ТС), дина.

Между перечисленными единицами силы существуют следующие зависимости:

1Н=105дин=0,102кг.

Графически силу изображают отрезком прямой со стрелкой; длина отрезка в определенном масштабе равна модулю вектора силы.

Масштаб силы: сколько единиц модуля силы содержится в единице длины ее вектора

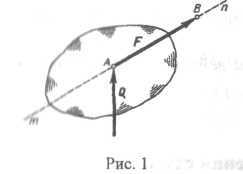
На рис. 1 изображена сила, приложенная в точке А и действующая по линии тп. Вектор силы обозначается, как правило, буквой с черточкой над ней (F), а модуль без черточки (F). Для силы F точка А называется началом, а точка В концом вектора. Нередко удобно изображать вектор силы так, чтобы стрелка, стоящая в конце вектора, упиралась в точку приложения силы (сила Q).

Системой сил называется сово­купность нескольких сил, приложенных к телу, в точке или системе тел и точек.

Система сил, линии действия которых лежат в различных плоскостях, называется пространственной, а в одной плоскости - плоской.

Система сил, с пересекающимися в одной точке линиями действия, называется сходящейся, которая может быть плоской и пространственной.

Различают также систему параллельных сил как частный слу­чай произвольно расположенных сил, в которых линии действия сил не схо­жи в одной точке.

Они также могут быть плоскими и пространственными.

В статике решаются следующие три основные задачи:

1. Приведение данной системы сил к другой, более простой, статистически эквивалентной системе;

2. Нахождение условий равновесия данной системы сил;

3.Определение сил взаимодействия между материальными объектами.

Аксиомы статики

В основе статики лежит ряд основных положений, полученных в ре­зультате наблюдений, опыта и практической деятельности людей. На ос­новании этих положений, называемых аксиомами статики, путем строгих математических доказательств делаются все последующие выводы.1 аксиома статики, получившая название аксиомы инерции, за­ключается в следующем:

Аксиома 1. Изолированная материальная точка находится в состоя­нии покоя или движется равномерно и прямолинейно.

Согласно этой аксиоме, материальная точка может двигаться равно­мерно и прямолинейно без приложенной к ней силы (по инерции). Изме­нить состояние покоя или равномерного прямолинейного движения мате­риальной точки может только сила.

Упомянутые два состояния точки объединяются в общем понятии "равновесие".

Аксиома 2. Две силы, приложенные к твердому телу, взаимно урав­новешиваются только тогда, когда они равны по величине и направлены по одной прямой в противоположные стороны (рис. 1.1).

 

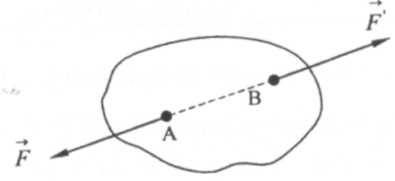
Из этой аксиомы и рис. 1.1. следует, что при равновесии рассмат­риваемого тела F = F Рис. 1.1

Аксиома 3. Две силы, приложенные к твердому телу в одной точке, имеют равнодействующую, приложенную в этой же точке и изображаются диагональю параллелограмма, построенного на этих силах, как на сторонах.

 

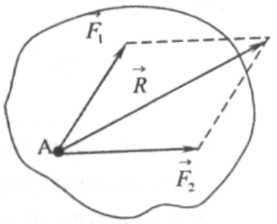
На рис 1.2 показана равнодействующая R двух сил F1 и F2, при­ложенных к твердому телу в точке А. Операция замены системы сил её равнодействующей называется сложени­ем данной системы сил.

Мы видим, что сложение двух сил, приложенных к твердому телу в одной точке, подчиняется правилу векторного сложения, чем подтверждается вы­сказанное предположение о том, что сила есть вектор.

Таким образом, равнодействующая двух сил, приложенных к твердому телу в одной точке, равна их векторной сумме, т.е. ¯R = ¯F1+¯F2. (1.1)

Аксиома 4. Присоединение или отбрасывание взаимно уравновеши­вающихся сил не изменяет действия данной системы сил на твердое тело.

Например, если Q=Q, то системы сил, показанные на рис. 1.3, ста­тически эквивалентны, так как на основании аксиомы 2 силы Q и Q/ вза­имно уравновешиваются и, следовательно, в силу аксиомы 4, их можно присоединить или отбросить.

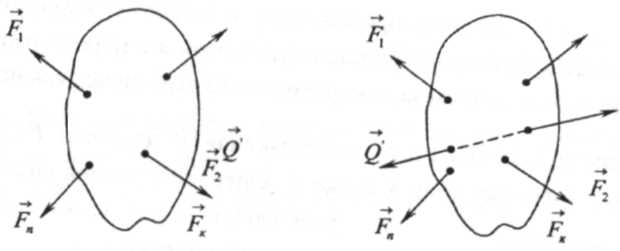
Рис. 1.3

Аксиома 5. Если каждая из двух систем статически эквивалентна одной и той же третьей системе, то они статически эквивалентны между собой. Понятно, что если система сил А статически эквивалентна системе С, и в то же время система В статически эквивалентна системе С, то и сис­темы А и В статически эквивалентны одна другой.

Из приведенных аксиом вытекают следующие следствия.

Следствие 1. Не изменяя действия силы на твердое тело, можно пе­реносить её точку приложения вдоль линии действия на любую точку тела.

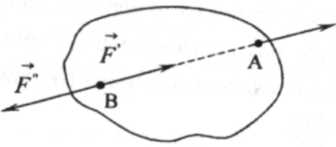
Рис. 1.4

В самом деле, три одинаковые по модулю силы F , F / и —► F ? / (рис. 1.4), направленные вдоль прямой, проходящие через точки А и В, статически эквивалентны, с одной стороны, силе F, так как силы F и F" взаимно уравновешиваются, и с другой стороны, силе и F , так как уравновешиваются силы F и F'/ . Следовательно, статически эквивалентны силы F и F"', т.е. точку А приложения силы F можно переносить вдоль её линии в любую точку В твердого тела.

Такие векторы, которые по их физическому смыслу можно перено­сить вдоль прямых, по которым они направлены, называются скользящими векторами.

Следовательно, сила есть вектор скользящий.

Следствие 2. Сила ¯R (рис. 1.5) равная по модулю равнодействующей ¯R и направленная по одной с ней прямой в противоположную сторо­ну, уравновешивает данную систему сил.

 

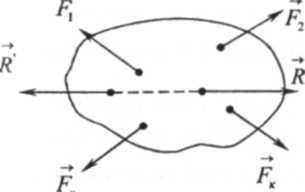
Поскольку сила R/ уравновешивает равнодействующую R, то она уравновешивает и статистически экви­валентную ей систему сил. F1 F2 ….Fn

Шестая аксиома, называемая аксиомой действия и противодействия, заключается в следующем:

Аксиома 6. Силы взаимодействия любых двух материальных объек­тов всегда равны по величине и направлены по одной прямой в противопо­ложные стороны.

 ¯ F¯ F?¯  

Эта аксиома, сформулированная Ньютоном, означает, что если объект А (рис. 1.6) действу­ет на объект В и это действие выражается силой F , то объект В оказывает объекту А противодействие, выраженное силой F/ , причем F = - F'.

Таким образом, всякой силе, приложенной к некоторому материаль­ному объекту, соответствует равная ей по модулю и прямо противополож­ная по направлению сила, приложенная к другому объекту, взаимодействующему с данным. Подчеркнем, что силы действия и противодействия не уравновешивают друг друга, так как они приложены к различным объектам.

Седьмая аксиома называется аксиомой отвердения. Она заключается в следующем:

Аксиома 7. Если нетвердое тело находится в равновесии под дейст­вием приложенных к нему сил, то равновесие его не нарушается при его отвердении.

Из этой аксиомы следует, что если нетвердое тело находится в равновесии под действием прило­женных к нему сил, то под действием этой же системы сил будет находиться в равновесии и Рис. 1.7 соответствующее абсолютно твердое тело.

 

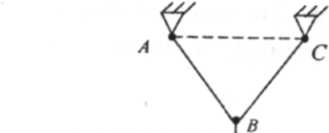
Например, если нить ABC (рис. 1.7), закрепленная в точках А и С, находится в равновесии под действием приложенной к ней вертикальной

силы F, то под действием этой же силы будет находиться в равновесии и абсолютно твердое тело, имеющее такую же форму. Обратное заключение сделать нельзя, т.е. из того, что под действием некоторой системы сил на­ходится в равновесии абсолютно твердое тело, вовсе не следует, что под действием этой же системы сил будет находиться в равновесии и любое нетвердое тело.

Например, если к нити, показанной на рис. 1.7 приложить в. точке В силу, направленную по вертикали вверх, то она не будет находиться в рав­новесии, тогда как соответствующее абсолютное твердое тело и в этом случае будет находиться в равновесии.

Из этого следует, что вместо равновесия реально сущест­вующих тел, можно рассматривать равновесие соответствующих абсолют­но твердых тел.

Этими аксиомами и следствиями из них мы будем пользоваться при изложении последующих тем статики, в которых рассматриваются различ­ные виды систем сил, приложенных к материальному объекту.

Простейшей из таких систем является система сходящихся сил.

Система сходящихся сил.

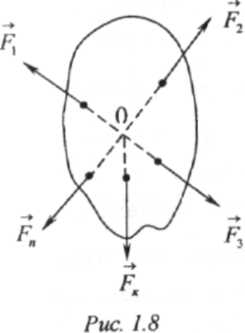
Ранее были рассмотрены аксиомы статики и их основные определения. Теперь перейдем к изу­чению простейшей системы сил. Такой системой является система сходящихся сил, т.е. таких сил, линии которых пересекаются в одной точке (рис. 1.8).Если линии действия всех сил такой системы расположены в одной плоскости, то система назы­вается плоской системой сходящихся сил. В про­тивном случае эта система называется простран­ственной системой сходящихся сил.

 Приведение системы сходящихся сил к простейшему виду

а) Геометрический метод сложения сходящихся сил .

Термин "сложить систему сил" означает - найти её равнодействую­щую. Задачи о сложении и равновесии сходящих­ся сил впервые решены Вариньоном. Начнем решение с поставленной задачи со случая сложения двух сходящихся сил. Пусть в точках А и В (рис. 1.9) к твердому телу приложе­ны две силы F1 и F2, линии действия которых пе­ресекаются в точке О. 

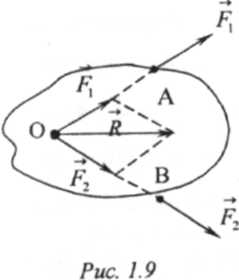
Поскольку сила является вектором скользящим, то перенося каждую из данных сил F1и F2 вдоль их действия в точку О, получим две силы, приложенные к твердому телу в одной точке О. Сложив их, на основании аксиомы 3, получим равнодействующую А, приложен­ную в этой точке и изображенную диагональю параллелограмма, постро­енного на этих силах, как на сторонах. Такой способ сложения двух схо­дящихся сил называется правилом параллелограмма сил.

Эта же задача также может быть решена с помощью правила треугольника сил, заключающего­ся в следующем (рис. 1.10). -

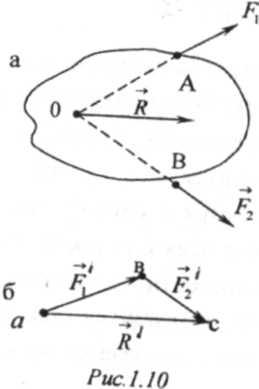
Из произвольной точки а (рис. 1.10б) проведем вектор f/=f, и из конца его b вектор f1=F2. Соединив точку а с концом вектора f2, получим вектор r', равный рав­нодействующей r данных сил. Последняя сила приложена в точке 0 пересечения линий действия данных сил f, и f2.

Теперь допустим, что требуется сложить систему сходя­щихся сил f1, f2 f,3 приложенных к твердому телу в различных его точках a1, а2, ...ап (рис. 1.11).

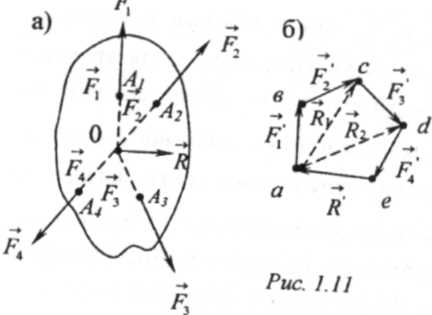
Перенеся все силы вдоль их линий действия в общую их точку пере­сечения, получим систему сил приложенных к данному телу в одной точке 0. Для сложения сил воспользуемся методом последовательного их сложе­ния.

Сложим сначала силы f1 и f2, использовав правило треугольника сил. Для этого из произвольной точки а (рис. 1.11б) проведем последовательно векторы F1f2 , равные соответственно векторам f1 и f2. Равнодействующая этих сил равна век­тору r', проведенному из точки а в конец с вектора f2 , и приложена в точке 0 пересечения линий дей­ствия данных сил (рис. 1.11а), причем r, =F1 +f2 . На рис. 1.11 б вектор R, показан пунктиром. Теперь, найденную равнодействующую r, сложим со следующей силой f3. Для этого из конца с вектора r1 проведем вектор f2 =f3. Тогда вектор R2 (см. пунктир на рис. 1.116), проведенный из точки а в конце d вектора F3, будет равен равнодействующей сил R, и F3, т.е. трех сил F 1F2, F3, причем R 2=R1 +F3,=Ft +F2 +F3. Приложена эта равнодействую­щая также в точке 0 (на рис. 1.11а) равнодействующие R2 и R1, не показа­ны. Аналогично складывая равнодействующую R2 последовательно со всеми остальными силами данной системы, получим равнодействующую r всех данных сил, приложенную в точке 0 и равную r = R/ =F1+F2'+F3'+...+ Fп' =ΣFк,

где R' - вектор, проведенный из точки а в конец е последнего из векторов, построенных на рис. 1.116.

Учтя, что Fk=Fk (к=1,2,...п), окончательно получим r = ΣFк. .

Сумма, стоящая в правой части этого равенства, называется векторной суммой сил.

Как нетрудно видеть, для построения вектора r равнодействующей системы сходящихся сил достаточно, начиная от произвольной точки а провести последовательно один за другим векторы f1,f2,...,fп, равные со­ответственно векторам данной системы сил F, ,F2 ,.. fп, из точки а про­вести вектор r в конец е последнего из проведенных векторов и затем перенести его параллельно в точку 0 пересечения линий действия данных сил. Многоугольник abcde называется многоугольником сил, а такой способ сложения системы сходящихся сил получил название правила многоуголь­ника. Вектор r , направленный противоположно всем остальным сторо­нам многоугольника adcde при обходе его периметра, называется замы­кающей стороной многоугольника сил.

Таким образом, равнодействующая системы сходящихся сил равна замыкающей стороне многоугольника сил, построенного на данных силах, как на сторонах, или векторной сумме этих сил, и приложена в точке пере­сечения их линий действия.

Заметим, что описанный способ применим не только для сложения плоской системы сходящихся сил. Им можно также пользоваться и при сложении сходящихся сил, не лежащих в одной плоскости, хотя в послед­нем случае применение его очень неудобно, так как трудно изобразить на плоскости пространственный многоугольник сил.

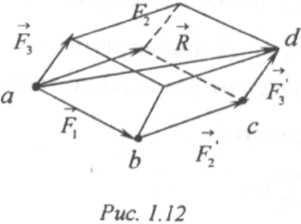
Особого внимания заслуживает сложение трех сходящихся сил, ли­нии действия которых не лежат в одной плоскости. Пусть дана пространственная система трех сходящихся сил F1, F2, F3, (рис. 1.12). Построим на этих силах пространственный многоугольник сил abсd (точка а этого многоугольника совмещена с точкой приложения сил данной системы).

Его замыкающая сторона ad = R равна по величине и направлению равнодействующей данных сил. Достроив этот многоугольник до параллелограмма, как это показано на рисунке, убедим­ся, что вектор равнодействующей R изображается его диагональю, а векторы данных сил F1, F2 и F3 - ребрами, исходящими из той же верши­ны d, из которой проведен вектор r .

Таким образом, приходим к выводу, что равнодействующая трех сходящихся сил, линии действия которых не лежат в одной плоскости, изображается диагональю параллелепипеда, по­строенного на данных силах, как на ребрах, исходящих из общей вершины.

б) Векторное условие равновесия системы сходящихся сил

Пусть r - равнодействующая системы сходящихся сил F1, F2, ..,Fп-1, (рис. 1.13).

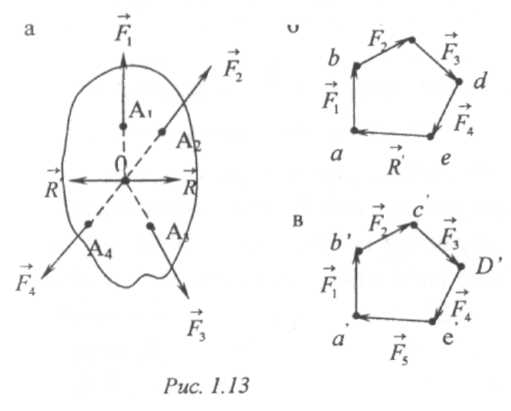
Поскольку сила R ', равная по модулю равнодействующей R и направленная по той же прямой в противоположную сторону, уравновешивает данную систему сил, то, присоединив к данной системе сил Fп = r (на рис. 1.13 силу F5) , мы получим взаимно уравновешенную систему сил F1, F2 , .., Fп (на рис. 1.13 систему F1 F2, .., Fп).

Если теперь вектор Fn присоединить к ломаной кривой abсde, то конец его совпадает с началом а вектора первой силы F, (рис. 1.1 Зв). Многоугольник сил abсdea, стороны которого направлены при обходе вдоль его периметра в одном и том же направлении, называется замкнутым. Равнодействующая такой системы сил равна нулю.

Следовательно, если система сходящихся сил вза­имно уравновешивается, то соответствующий много­угольник сил замкнут и рав­нодействующая или вектор­ная сумма сил равна 0.

Таким образом, необходимым усло­вием равновесия системы сходящихся сил является равенство 0 векторной суммы данных сил. Это условие является также и достаточным.

В самом деле, если дана система сходящихся сил F1, F2, .., Fп, век­торная сумма которых равна нулю (рис. 1.13в), то, заменив силы F,, F2, .., Fп-1 , их равнодействующей

R= -Fп приложенной в точке 0 (рис. 1.13а), будем иметь две равные и противоположно направленные по одной пря­мой силы R и r =F„, которые, на основании аксиомы 2, взаимно урав­новешиваются. Следовательно, уравновешивается и система сил F1, F2, .., Fп.

Та­ким образом, векторным условием равновесия системы сходящихся сил является векторное равенство: ΣFt=0, что означает, что многоугольник сил, построенный на силах данной систе­мы, должен быть замкнутым.

 Разложение силы на составляющие, приложенные в её точке приложения

Теперь решим обратную задачу. Пусть задана сила¯F, приложенная в некоторой точке А. Требуется разложить её на составляющие, приложен­ные в этой же точке.

Рассмотрим сначала случай разложения силы F на две составляю­щие F1 и F2 (рис. 1.14). Эта задача сводится к построению параллелограм­ма, диагональю которого изображался бы вектор данной силы. Таких паралле­лограммов можно построить бесчислен­ное множество. Следовательно, постав­ленная задача является многозначной. Чтобы сделать её однозначной, необхо­димо задать дополнительные условия.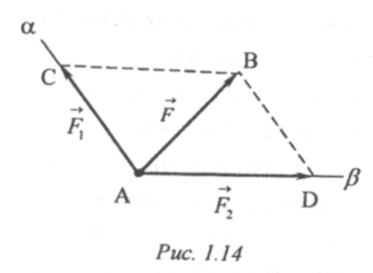  

Наиболее часто встречается задача о разложении силы на две составляющие, приложенные в её точке приложения, по заданным линиям действия иско­мых составляющих.

Пусть силу ¯F, приложенную в точке А (рис. 1.14), требуется разло­жить на две составляющие, приложенные в этой же точке и направленные по заданным прямым Аа и Аβ. Для решения этой задачи достаточно из конца В вектора F провести прямые ВД и ВС, параллельные соответст­венно прямым Аа и Аβ Тогда стороны АС и AD построенного таким обра­зом параллелограмма ABCD изобразят векторы искомых составляющих F1 и F2.

Для разложения силы на две составляющие, приложенные в её точке приложения, могут быть также заданы величины составляющих сил или величина и линия действия одной из них и, наконец, величина одной и ли­ния другой. Во всех этих случаях задача решается путем геометрического построения параллелограмма сил. Предлагается самостоятельно рассмот­реть все эти случаи и выяснить, при каких условиях каждая из этих задач является однозначной, двузначной или не имеет решений.

Рассмотрим теперь случай разложения силы на три некомпланарные составляющие, приложенные в её же точке приложения. Эта задача сво­дится к построению параллелепипеда, диагональю которого изображался бы вектор данной силы, и в общем случае также является многозначной. Для того чтобы сделать её однозначной, необходимо задать дополнитель­ные условия. Наиболее важным является случай разложения силы на три некомпланарные составляющие, приложенные в одной с ней точке, по за­данным линиям действия всех трех составляющих.